（同步复习精讲辅导）北京市2014-2015学年高中数学 点线面综合问题课后练习一（含解析）新人教A版必修2

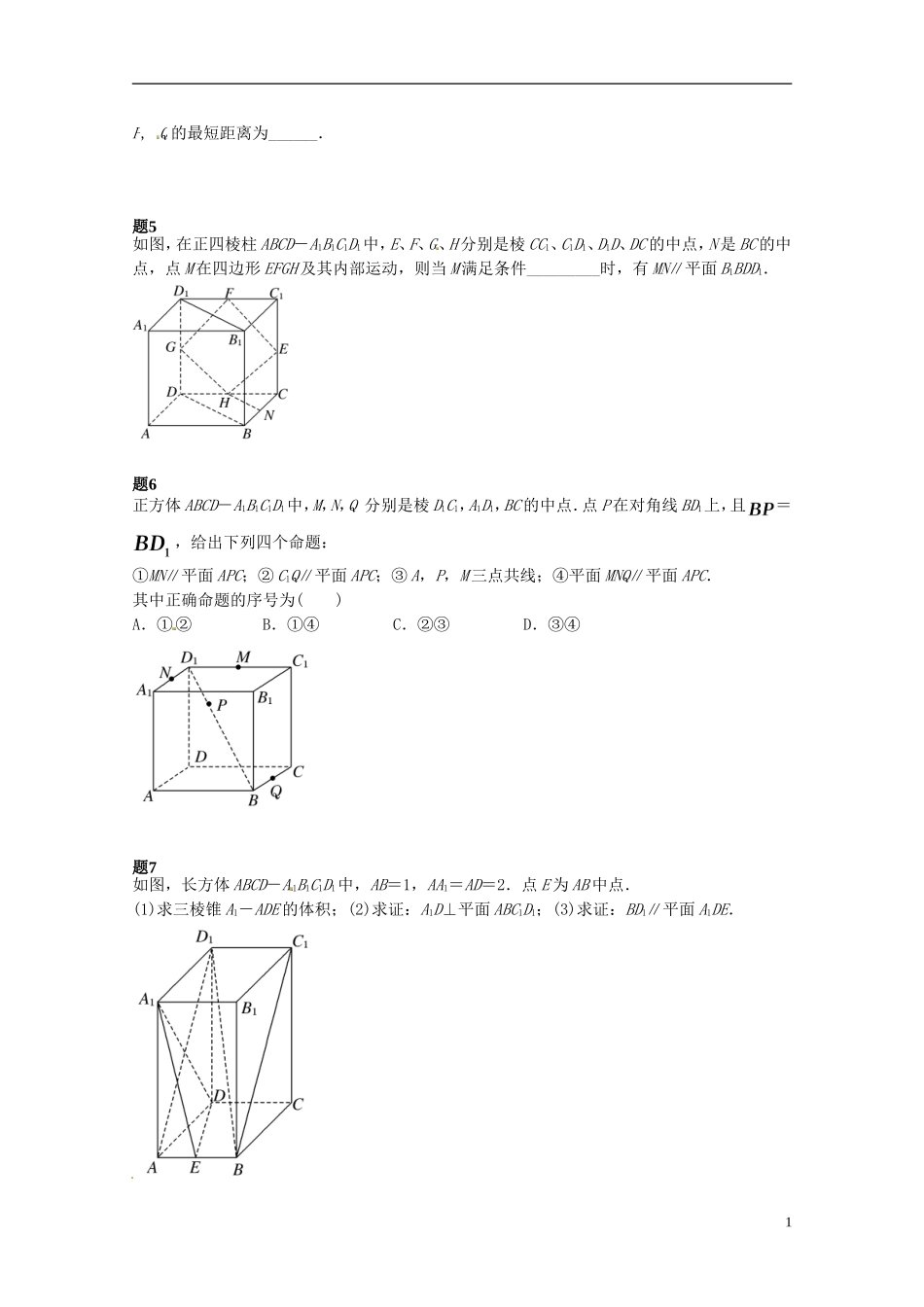
（同步复习精讲辅导）北京市 2014-2015 学年高中数学 点线面综合问题课后练习一（含解析）新人教 A 版必修 2如图所示，在边长为 12 的正方形中，点 B、C 在线段 AD 上，且 AB = 3，BC = 4,作分别交于点 B1，P，作分别交于点，将该正方形沿折叠，使得与重合，构成如图 2 所示的三棱柱．(I)求证：平面；(II)求多面体的体积．题1已知 a、b 是异面直线，直线 c∥直线 a，则 c 与 b( )A．一定是异面直线 B．一定是相交直线C．不可能是平行直线 D．不可能是相交直线题2设 、 、 是三个互不重合的平面，m 、n 是两条不重合的直线，下列命题中正确的是（ ）．A．若，，则B．若//m  ，//n ，，则 mnC．若，m，则//mD．若// ， m，//m  ，则//m题3圆柱的轴截面(经过圆柱的轴所作的截面)是边长为 5cm 的正方形 ABCD，则圆柱侧面上从 A 到 C的最短距离为( )．A．10cmB．cm C．cmD．cm题4空间四边形 ABCD 的各边及两条对角线的长都是 1,点 M 在边 AB 上移动,点 Q 在边 CD 上移动，则0P, Q 的最短距离为______．题5如图，在正四棱柱 ABCD－A1B1C1D1中，E、F、G、H 分别是棱 CC1、C1D1、D1D、DC 的中点，N 是 BC 的中点，点 M 在四边形 EFGH 及其内部运动，则当 M 满足条件_________时，有 MN∥平面 B1BDD1．题6正方体 ABCD－A1B1C1D1中，M，N，Q 分别是棱 D1C1，A1D1，BC 的中点．点 P 在对角线 BD1上，且＝，给出下列四个命题：①MN∥平面 APC；② C1Q∥平面 APC；③ A，P，M 三点共线；④平面 MNQ∥平面 APC．其中正确命题的序号为( )A．① ② B．①④C．②③ D．③④题7如图，长方体 ABCD－A 1B1C1D1中，AB＝1，AA1＝AD＝2．点 E 为 AB 中点．(1)求三棱锥 A1－ADE 的体积；(2)求证：A1D⊥平面 ABC1D1；(3)求证：BD1∥平面 A1DE．1题8设四棱锥 P－ABCD 的底面不是平行四边形，用平面 α 去截此四棱锥(如图)，使得截面四边形是平行四边形，则这样的平面 α( )．A．不存在 B．只有 1 个 C．恰有 4 个 D．有无数多个2课后练习详解题1答案：见详解．详解：（Ⅰ）证明：由题知：3AB  ，4BC  ，5CA  ，∴ ABBC．又 1ABBB，∴ AB 平面11BCC B ；（Ⅱ）由题知：三棱柱111ABCA B C的体积13 4 12722   ． ABP和 ACQ都是等...