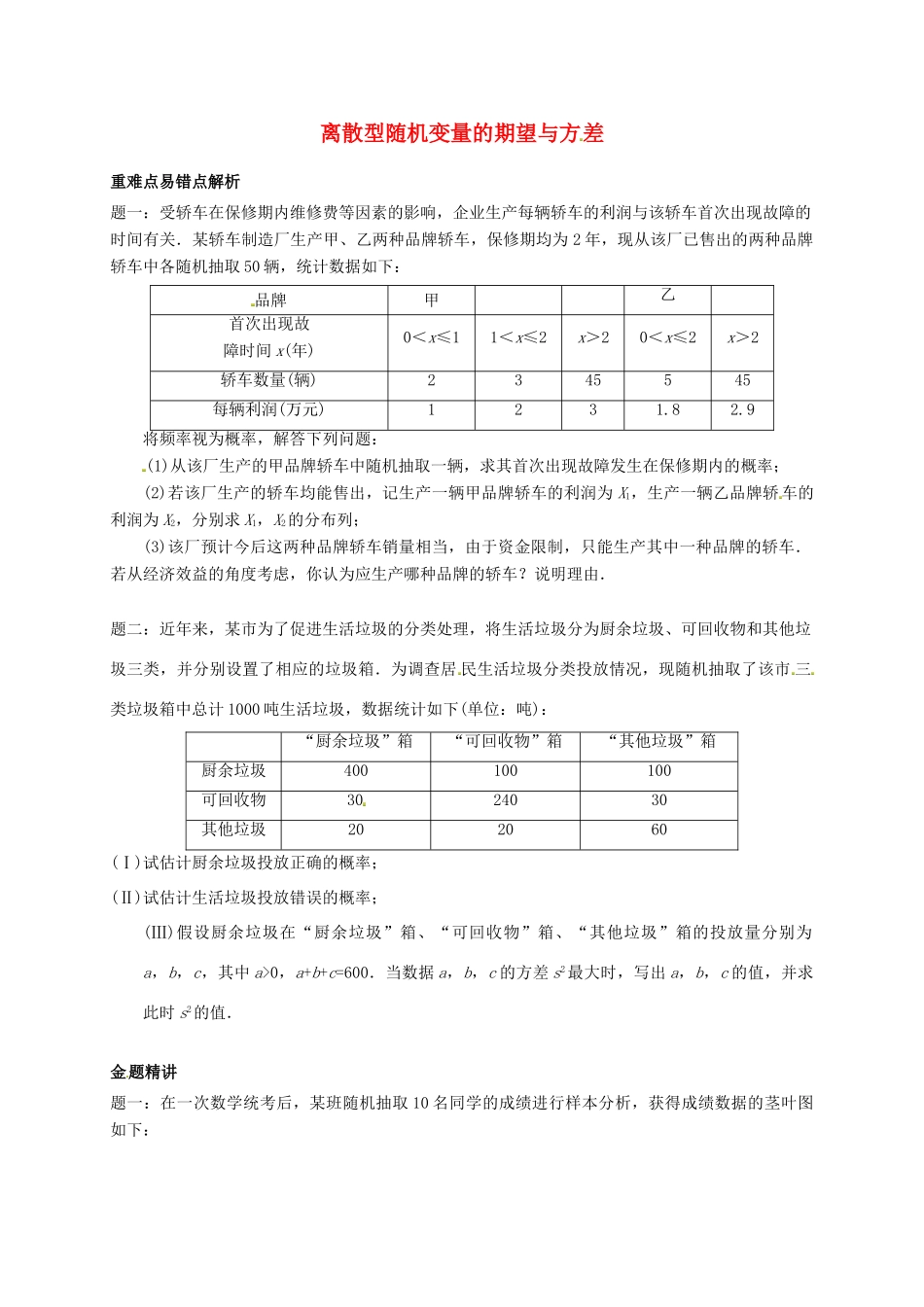
离散型随机变量的期望与方差重难点易错点解析题一:受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为 2 年,现从该厂已售出的两种品牌轿车中各随机抽取 50 辆,统计数据如下:品牌甲乙首次出现故障时间 x(年)0<x≤11<x≤2x>20<x≤2x>2轿车数量(辆)2345545每辆利润(万元)1231.82.9将频率视为概率,解答下列问题:(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为 X1,生产一辆乙品牌轿车的利润为 X2,分别求 X1,X2的分布列;(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.题二:近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居 民生活垃圾分类投放情况,现随机抽取了该市 三类垃圾箱中总计 1000 吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400100100可回收物3024030其他垃圾202060(Ⅰ)试估计厨余垃圾投放正确的概率;(Ⅱ)试估计生活垃圾投放错误的概率;(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中 a>0,a+b+c=600.当数据 a,b,c 的方差 s2最大时,写出 a,b,c 的值,并求此时 s2的值.金题精讲题一:在一次数学统考后,某班随机抽取 10 名同学的成绩进行样本分析,获得成绩数据的茎叶图如下:00444558826789(1)计算样本的平均成绩及方差;(2)现从这 10 个样本中随机抽出 2 名学生的成绩,设选出学生的分数为 90 分以上的人数为 X,求随机变量的分布列和均值.题二 :为了考察某校各班参加课外书法小组的人数,在全校随机抽取 5 个班级,把 每个班级参加该小组的人数作为样本数据.已知样本平均数为 7,样本方差为 4,且样本数据互不相同,则样本数据中的最大值为__________.题三:下图是 1,2,两组各 7 名同学体重(单位:kg)数据的茎叶图.设 1,2 两组数据的平均数依次为和,标准差依次为 s1和 s2,那么( )A. ,s1>s2 B. ,s1s2离散型随机变量的期望与方差讲义参考答案重难点易...