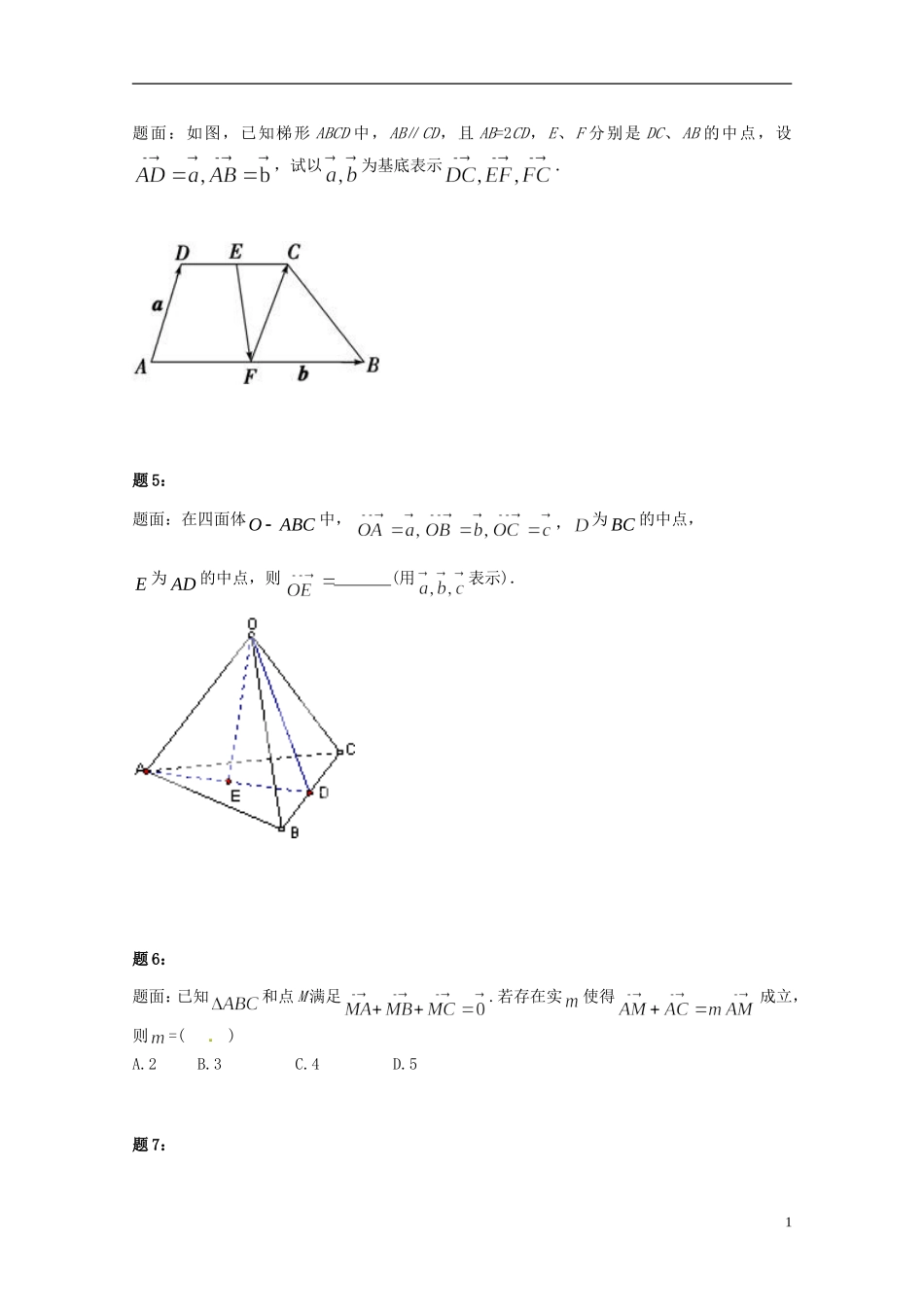
(同步复习精讲辅导)北京市 2014-2015 学年高中数学 平面向量的概念及线性运算课后练习二 新人教 A 版必修 4题 1:题面:下面四个命题:(1)所有的单位向量相等;(2)长度不等且方向相反的两个向量不一定是共线向量;(3)由于零向量的方向不确定,故与任何向量不平行;(4)对于任何向量,,必有|+|≤||+||.其中正确命题的序号为 .题 2:题面:对于 空间中的非零向量①;②;③;④其中一定不成立的是 .题 3:题面:三棱锥 P-ABC 中,M 为 BC 的中点,以为基底,则可表示为 ____. 题 4:0题面:如图,已知梯形 ABCD 中,AB∥CD,且 AB=2CD,E、F 分别是 DC、AB 的中点,设,试以为基底表示.题 5:题面:在四面体OABC中,,为 BC 的中点,E 为 AD 的中点,则 (用表示). 题 6:题面:已知和点 M 满足.若存在实使得成立,则=( )A.2B.3C.4D.5题 7:1题面:已知 O,N,P 在 ABC所在平面内,且,且,则点 O,N,P 依次是 ABC的 ( )A.重心 外心 垂心 B.重心 外心 内心 C.外心 重心 垂心 D.外心 重心 内心(注:三角形的三条高线交于一点,此点为三角型的垂心)题 8:题 面 :O是△ABC所在平面上的一定点,动点P满足λ∈[0,+∞),则点 P 形成的图形一定通过△ABC 的 .(填外心或内心或重心或垂心)课后练习详解题 1:2答案:(4).详解:(1)单位向量指模为 1 的向量,方向可为任意的,故错误;(2)由共线向量的定义,方向相反的两个向量一定是共线向量,故错误;(3)规定:零向量与任何向 量为平行向量,故错误;(4)因为|+|2=2+2+2•≤2+2+2||•||=(||+||)2,故正确故答案为:(4).题 2:答案:②.详解:根据空间向量的加减法运算,对于①:恒成立;对于②:,即②不成立;对于③:当方向相同时,有;对于④:当共线且与方向相反时,有.故答案为:②.题 3:答案:.详解:在△ABC 中,M 为 BC 的中点,则由平行四边形法则得3题 4:答案:.详解:∵DC∥AB,AB=2DC,E、F 分别是 DC、AB 的中点,题 5:答案: 详解:因为 D 是 BC 的中点,E 是 AD 的中点,题 6:答案:B4详解:由知,点 M 为△ ABC 的重心,设点 D 为底边 BC 的中点,题 7:答案: C详解:由值,O 为△ABC 的外心;由知,O 为△ABC 的重心.∵ ∴,∴∴同理 ,∴P 为△ABC的垂心.题 8:答案:垂心.详解:,,∵,5∴点 P 在 BC 的高线上,即 P 的轨迹过△ABC 的垂心故答案为:垂心.6