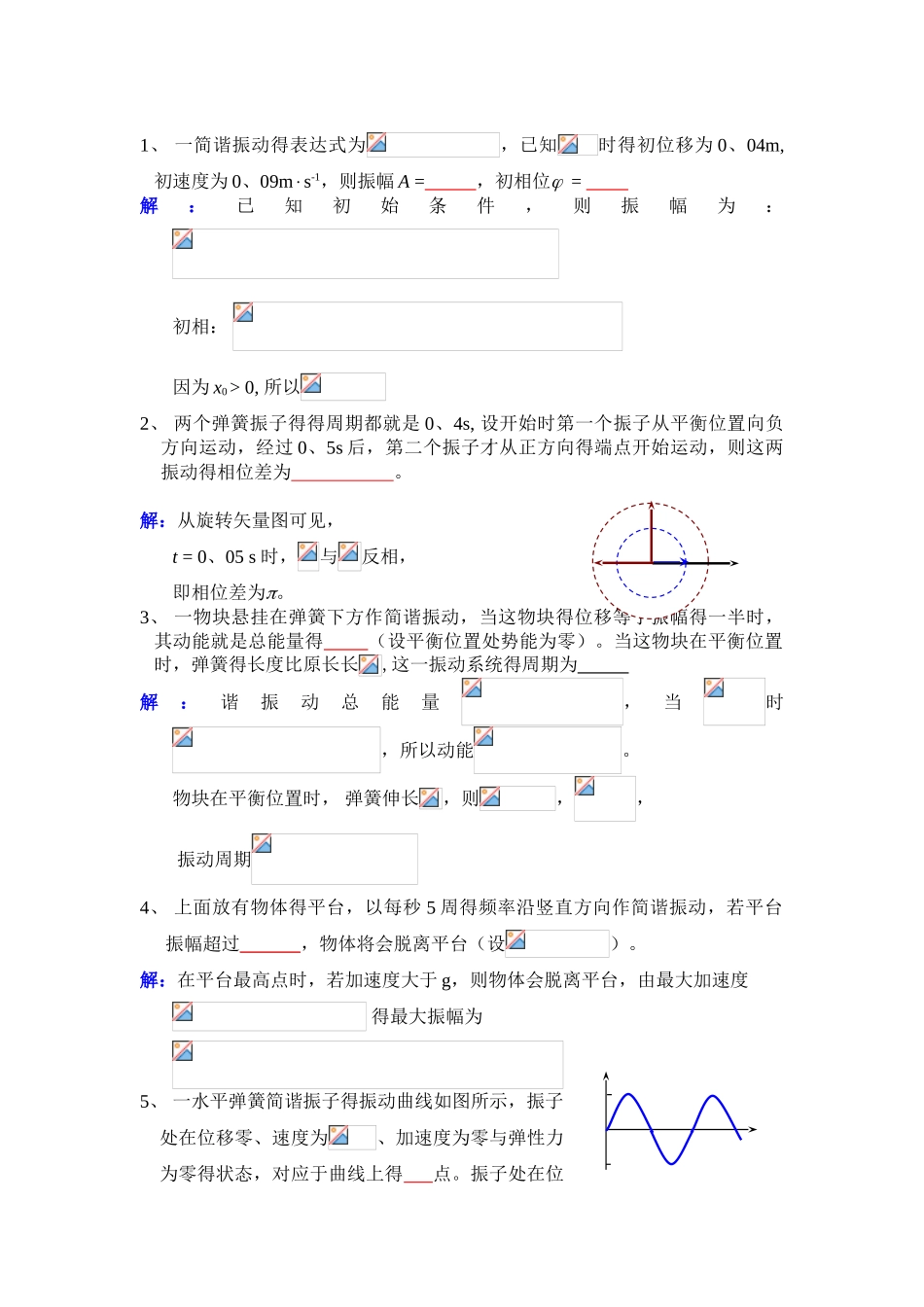
1、 一简谐振动得表达式为,已知时得初位移为 0、04m, 初速度为 0、09ms-1,则振幅 A = ,初相位 = 解:已知初始条件,则振幅为:初相: 因为 x0 > 0, 所以2、 两个弹簧振子得得周期都就是 0、4s, 设开始时第一个振子从平衡位置向负方向运动,经过 0、5s 后,第二个振子才从正方向得端点开始运动,则这两振动得相位差为 。解:从旋转矢量图可见,t = 0、05 s 时,与反相, 即相位差为。3、 一物块悬挂在弹簧下方作简谐振动,当这物块得位移等于振幅得一半时,其动能就是总能量得 (设平衡位置处势能为零)。当这物块在平衡位置时,弹簧得长度比原长长,这一振动系统得周期为 解:谐振动总能量,当时 ,所以动能。物块在平衡位置时, 弹簧伸长,则,,振动周期 4、 上面放有物体得平台,以每秒 5 周得频率沿竖直方向作简谐振动,若平台振幅超过 ,物体将会脱离平台(设)。解:在平台最高点时,若加速度大于 g,则物体会脱离平台,由最大加速度 得最大振幅为5、 一水平弹簧简谐振子得振动曲线如图所示,振子处在位移零、速度为、加速度为零与弹性力为零得状态,对应于曲线上得 点。振子处在位移得绝对值为 A、速度为零、加速度为-2A 与弹性力-kA 得状态,对应于曲线得 点。解:位移,速度,对应于曲线上得b、f 点;若|x|=A, ,又, 所以 x = A,对应于曲线上得 a、e点。6、 两个同方向同频率得简谐振动,其振动表达式分别为: (SI) 与 (SI)它们得合振动得振幅为 ,初相位为 。解:将 x2改写成余弦函数形式:由矢量图可知,x1与 x2反相,合成振动得振幅,初相三、计算题1、 一质量 m = 0、25 kg 得物体,在弹簧得力作用下沿 x 轴运动,平衡位置在原点、 弹簧得劲度系数 k = 25 N·m-1. (1) 求振动得周期 T 与角频率. (2) 假如振幅 A =15 cm,t = 0 时物体位于 x = 7、5 cm 处,且物体沿 x 轴反向运动,求初速 v0及初相. (3) 写出振动得数值表达式. 解:(1) 1 分 s 1 分 (2) A = 15 cm,在 t = 0 时,x0 = 7、5 cm,v 0 < 0 由 得 m/s 2 分 或 4/3 2 分 x0 > 0 ,∴ (3) (SI) 2 分(3) 振动方程为(SI)2、 在一平板上放一质量为 m =2 kg 得物体,平板在竖直方向作简谐振动,其振动周期为 T = s,振幅 A = 4 cm,求 (1) 物体对平板得压力得表达式. (2) 平板以多...