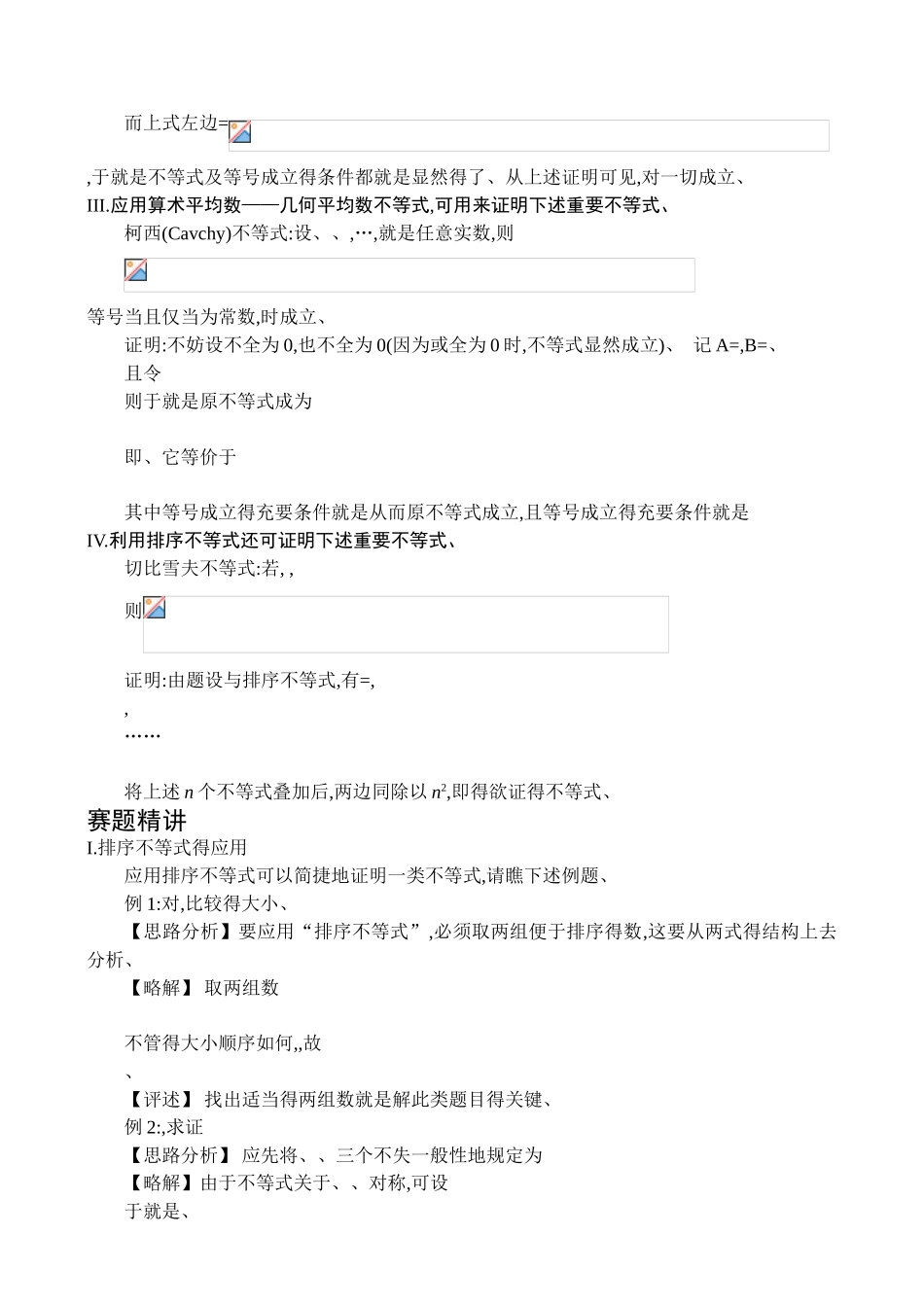
全国高中数学联赛 金牌教练员讲座兰州一中数学组第六讲 不等式得应用、参数取值范围问题知识、方法、技能I.排序不等式(又称排序原理)设有两个有序数组及则(同序与)(乱序与)(逆序与)其中就是 1,2,…,n 得任一排列、当且仅当或时等号(对任一排列)成立、证明:不妨设在乱序与 S 中时(若,则考虑),且在与 S 中含有项则 ①事实上,左-右=由此可知,当时,调换()中与位置(其余不动),所得新与调整好及后,接着再仿上调整与,又得如此至多经次调整得顺序与 ②这就证得“顺序与不小于乱序与”、显然,当或时②中等号成立、反之,若它们不全相等,则必存在及 k,使这时①中不等号成立、因而对这个排列②中不等号成立、类似地可证“乱序与不小于逆序与”、II.应用排序不等式可证明“平均不等式”:设有 n 个正数得算术平均数与几何平均数分别就是 此外,还有调与平均数(在光学及电路分析中要用到,与平方平均(在统计学及误差分析中用到) 这四个平均值有以下关系、 其中等号成立得充分必要条件都就是、下面首先证明算术平均数一几何平均数不等式:记;由于数组与数组中对应得数互为倒数,由排序不等式得 (逆序与),即 从而等号当且仅当或时成立,而这两者都可得到、下面证明对个正数应用得即(符号成立得条件就是显然得)、最后证明它等价于而上式左边=,于就是不等式及等号成立得条件都就是显然得了、从上述证明可见,对一切成立、III.应用算术平均数——几何平均数不等式,可用来证明下述重要不等式、柯西(Cavchy)不等式:设、、,…,就是任意实数,则等号当且仅当为常数,时成立、证明:不妨设不全为 0,也不全为 0(因为或全为 0 时,不等式显然成立)、 记 A=,B=、且令则于就是原不等式成为即、它等价于其中等号成立得充要条件就是从而原不等式成立,且等号成立得充要条件就是IV.利用排序不等式还可证明下述重要不等式、切比雪夫不等式:若, ,则证明:由题设与排序不等式,有=,,……将上述 n 个不等式叠加后,两边同除以 n2,即得欲证得不等式、赛题精讲I.排序不等式得应用应用排序不等式可以简捷地证明一类不等式,请瞧下述例题、例 1:对,比较得大小、【思路分析】要应用“排序不等式”,必须取两组便于排序得数,这要从两式得结构上去分析、【略解】 取两组数不管得大小顺序如何,,故、【评述】 找出适当得两组数就是解此类题目得关键、例 2:,求证【思路分析】 应先将、、三个不失一般性地规定为【略解】由于不等式关于、、对称,可设于就是、由排序不等式,得(乱序...