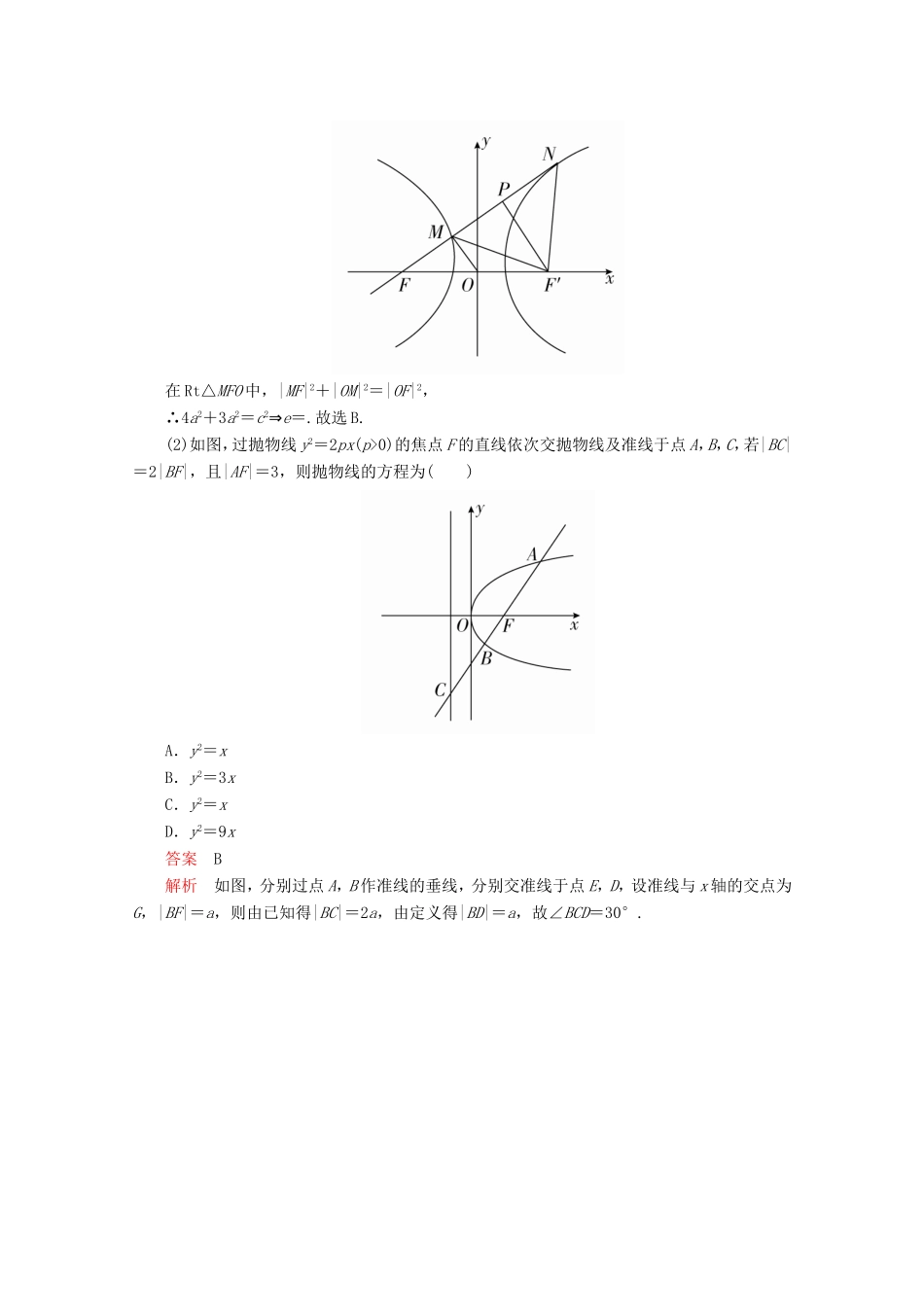
第2讲椭圆、双曲线、抛物线「考情研析」1.考查圆锥曲线的定义、方程及几何性质,特别是椭圆、双曲线的离心率和双曲线的渐近线.2.以解答题的形式考查直线与圆锥曲线的位置关系(弦长、中点等).核心知识回顾1.圆锥曲线的定义式(1)椭圆:|PF1|+|PF2|=2a(2a>|F1F2|);(2)双曲线:||PF1|-|PF2||=2a(2a<|F1F2|);(3)抛物线:|PF|=|PM|,点F不在直线l上,PM⊥l于M(l为抛物线的准线方程).2.圆锥曲线的重要性质(1)椭圆、双曲线中a,b,c之间的关系①在椭圆中:□a2=b2+c2;离心率为e==;②在双曲线中:□c2=a2+b2;离心率为e==.(2)双曲线的渐近线方程与焦点坐标①双曲线-=1(a>0,b>0)的渐近线方程为□y=±x;焦点坐标F1□(-c,0),F2□(c,0);②双曲线-=1(a>0,b>0)的渐近线方程为□y=±x,焦点坐标F1□(0,-c),F2□(0,c).(3)抛物线的焦点坐标与准线方程①抛物线y2=±2px(p>0)的焦点坐标为□,准线方程为□x=∓;②抛物线x2=±2py(p>0)的焦点坐标为□,准线方程为□y=∓.3.弦长问题(1)弦长公式设直线斜率为k,直线与圆锥曲线交于A(x1,y1),B(x2,y2)时,|AB|=|x1-x2|=或|AB|=|y1-y2|=.(2)过抛物线焦点的弦长过抛物线y2=2px(p>0)焦点F的弦AB,若A(x1,y1),B(x2,y2),则x1x2=,y1y2=-p2,弦长|AB|=□x1+x2+p.热点考向探究考向1圆锥曲线的定义和标准方程例1(1)(2019·永州市高三第三次模拟)过双曲线C:-=1(a>0,b>0)左焦点F的直线l与C交于M,N两点,且FN=3FM,若OM⊥FN,则C的离心率为()A.2B.C.3D.答案B解析设双曲线的右焦点为F′,取MN的中点P,连接F′P,F′M,F′N,如图所示,由FN=3FM,可知|MF|=|MP|=|NP|.又O为FF′的中点,可知OM∥PF′. OM⊥FN,∴PF′⊥FN.∴PF′为线段MN的垂直平分线.∴|NF′|=|MF′|.设|MF|=t,由双曲线定义可知|NF′|=3t-2a,|MF′|=2a+t,则3t-2a=2a+t,解得t=2a.在Rt△MF′P中,|PF′|===2a,∴|OM|=|PF′|=a.在Rt△MFO中,|MF|2+|OM|2=|OF|2,∴4a2+3a2=c2⇒e=.故选B.(2)如图,过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程为()A.y2=xB.y2=3xC.y2=xD.y2=9x答案B解析如图,分别过点A,B作准线的垂线,分别交准线于点E,D,设准线与x轴的交点为G,|BF|=a,则由已知得|BC|=2a,由定义得|BD|=a,故∠BCD=30°.在直角三角形ACE中, |AE|=|AF|=3,|AC|=3+3a,2|AE|=|AC|,∴3+3a=6,从而得a=1. BD∥FG,∴=,求得p=,因此抛物线的方程为y2=3x.(3)已知F是椭圆E:+=1(a>b>0)的左焦点,经过原点O的直线l与椭圆E交于P,Q两点,若|PF|=2|QF|,且∠PFQ=120°,则椭圆E的离心率为()A.B.C.D.答案C解析解法一:设F1是椭圆E的右焦点,如图,连接PF1,QF1.根据对称性,线段FF1与线段PQ在点O处互相平分,所以四边形PFQF1是平行四边形,|FQ|=|PF1|,∠FPF1=180°-∠PFQ=60°,根据椭圆的定义,|PF|+|PF1|=2a,又|PF|=2|QF|,所以|PF1|=a,|PF|=a,而|F1F|=2c,在△F1PF中,由余弦定理,得(2c)2=2+2-2×a×a×cos60°,得=,所以椭圆E的离心率e==.故选C.解法二:设F1是椭圆E的右焦点,连接PF1,QF1.根据对称性,线段FF1与线段PQ在点O处互相平分,所以四边形PFQF1是平行四边形,|FQ|=|PF1|,∠FPF1=180°-∠PFQ=60°,又|FP|=2|PF1|,所以△FPF1是直角三角形,∠FF1P=90°,不妨设|PF1|=1,则|FP|=2,|FF1|=2c===,根据椭圆的定义,2a=|PF|+|PF1|=1+2=3,所以椭圆E的离心率e==.故选C.圆锥曲线的定义、标准方程的关注点(1)准确把握圆锥曲线的定义和标准方程及其简单几何性质,注意焦点在不同坐标轴上时椭圆、双曲线、抛物线方程的不同表示形式.(2)求圆锥曲线方程的基本方法就是待定系数法,可结合草图确定.(3)焦点三角形的作用:借助焦点三角形能很好地将定义式与三角形中的边角关系式构建方程组,便于解决问题.(4)圆锥曲线基本问题的考查的另一个重点是定义的应用,根据圆锥曲线的定义分析判断一些问题,在椭圆、双曲线中如果已知曲线上一点与一个焦点的连线,则要把...