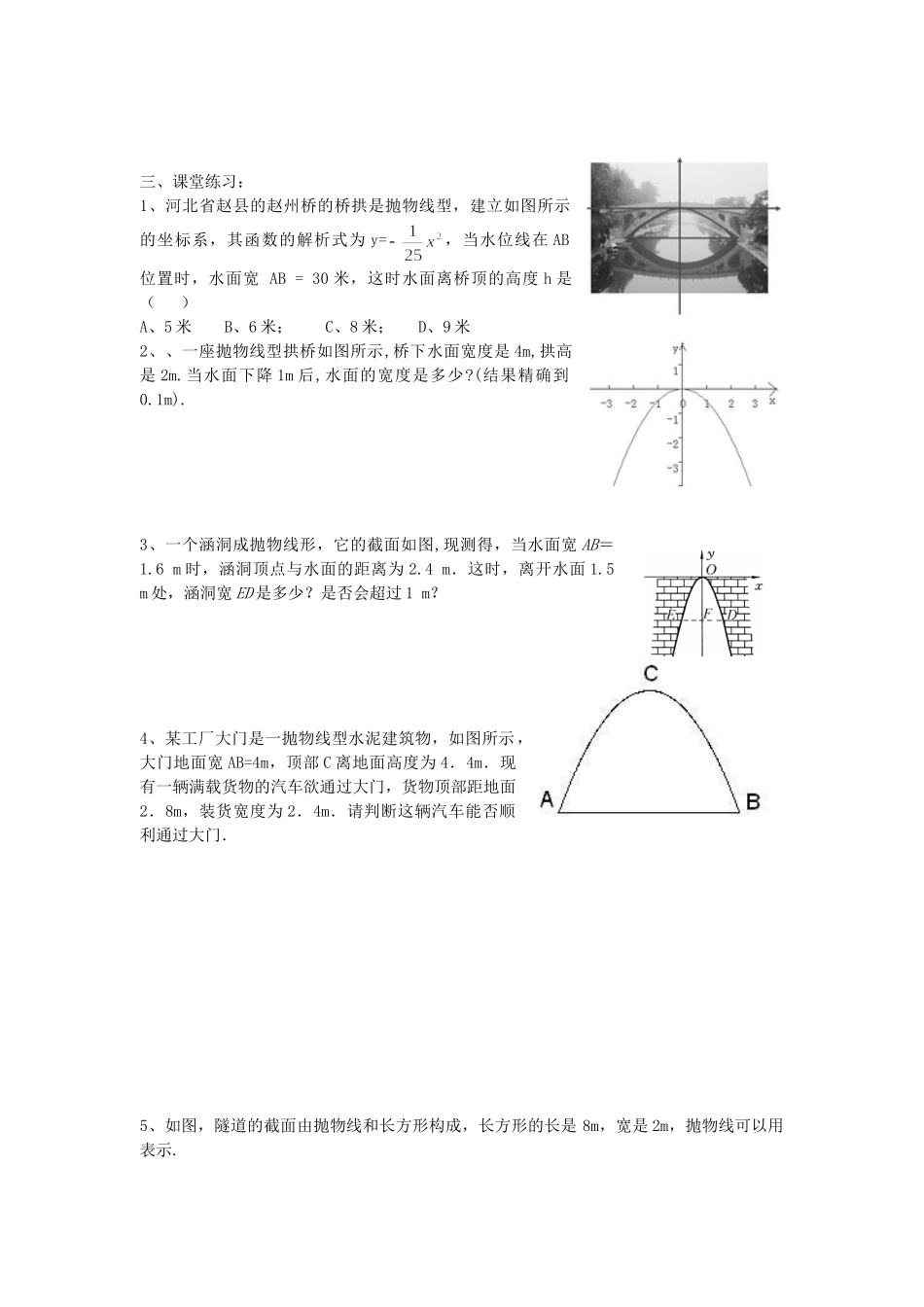
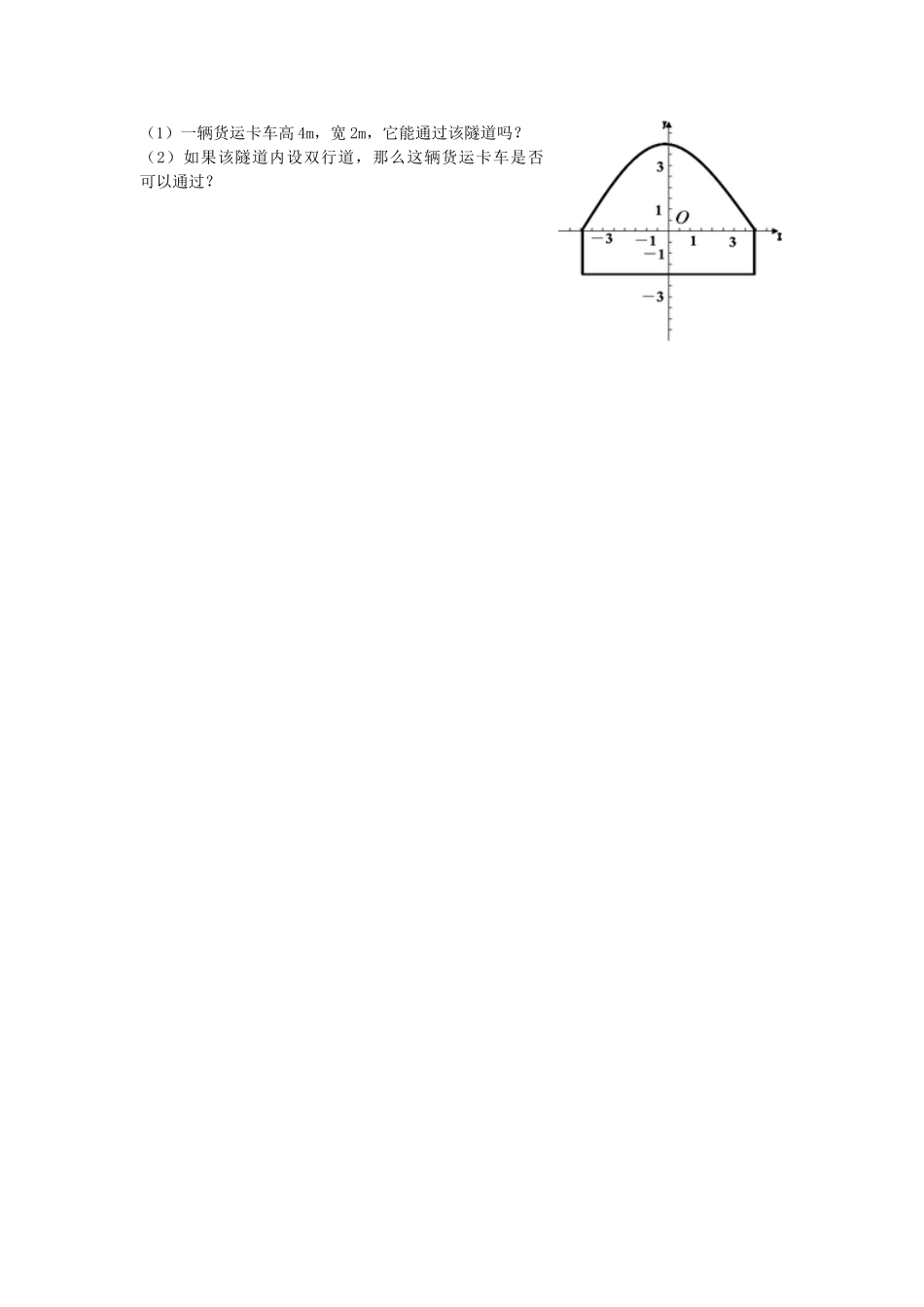
第 3 课时 拱桥问题和运动中的抛物线学习目标:1、体会二次函数是一类最优化问题的数学模型,了解数学的应用价值。2、掌握实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值、最小值。学习重点:应用二次函数最值解决实际问题中的最大利润。学习难点:能够正确地应用二次函数最值解决实际问题中的最大利润.特别是把握好自变量的取值范围对最值的影响。学习过程:一、预备练习:1、如图所示的抛物线的解析式可设为 ,若AB∥x 轴,且 AB=4,OC=1,则点 A 的坐标为 ,点 B的坐标为 ;代入解析式可得出此抛物线的解析式为 。2、 某涵洞是抛物线形,它的截面如图所示。现测得水面宽 AB=4m,涵洞顶点 O 到水面的距离为 1m,于是你可推断点 A 的坐标是 ,点 B 的坐标为 ;根据图中的直角坐标系内,涵洞所在的抛物线的函数解析式可设为 。二、新课导学:例 1、有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶 4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于 18m,求水面在正常水位基础上上涨多少米时,就会影响过往船只航行。例 2、某涵洞是抛物线形,它的截面如图所示,现测得水面宽 1.6m,涵洞顶点 O 到水面的距离为 2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?三、课堂练习:1、河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为 y=,当水位线在 AB位置时,水面宽 AB = 30 米,这时水面离桥顶的高度 h 是( ) A、5 米 B、6 米; C、8 米; D、9 米2、、一座抛物线型拱桥如图所示,桥下水面宽度是 4m,拱高是 2m.当水面下降 1m 后,水面的宽度是多少?(结果精确到0.1m).3、一个涵洞成抛物线形,它的截面如图,现测得,当水面宽 AB=1.6 m 时,涵洞顶点与水面的距离为 2.4 m.这时,离开水面 1.5 m 处,涵洞宽 ED 是多少?是否会超过 1 m?4、某工厂大门是一抛物线型水泥建筑物,如图所示,大门地面宽 AB=4m,顶部 C 离地面高度为 4.4m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为 2.4m.请判断这辆汽车能否顺利通过大门.5、如图,隧道的截面由抛物线和长方形构成,长方形的长是 8m,宽是 2m,抛物线可以用 表示.(1)一辆货运卡车高 4m,宽 2m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?