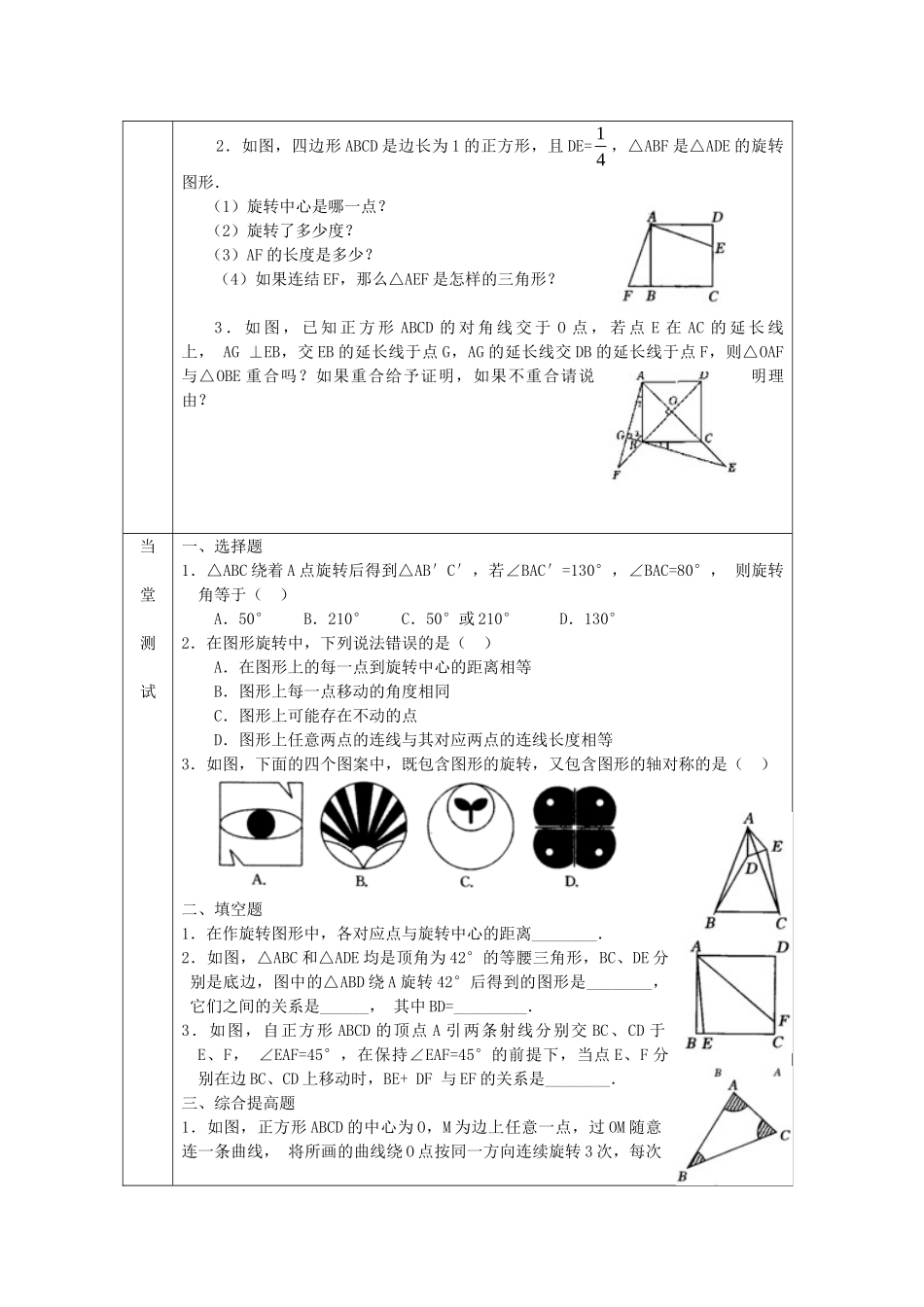
23.1 图形的旋转第 2 课时 旋转作图及变换学习目标1.理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用. 2.通过师生互动、合作交流以及动手操作过程,发现旋转变换所蕴含的美,激发学习数学的兴趣。学习重点图形的旋转的基本性质及其应用。学习难点运用操作实验几何得出图形的旋转的三条基本性质.教学准备激趣明标 1.什么叫旋转?什么叫旋转中心?什么叫旋转角? 2.什么叫旋转的对应点? 3.请独立完成下面的题目.如图,O 是六个正三角形的公共顶点,正六边形 ABCDEF 能否看做是某条线段绕 O 点旋转若干次所形成的图形? (老师点评)分析:能.看做是一条边(如线段 AB)绕 O 点,按照同一方法连续旋转 60°、120°、180°、240°、300°形成的.自主学习上面的解题过程中,能否得出什么结论,请回答下面的问题: 1.A、B、C、D、E、F 到 O 点的距离是否相等? 2.对应点与旋转中心所连线段的夹角∠BOC、∠COD、∠DOE、∠EOF、∠FOA 是否相等? 3.旋转前、后的图形这里指三角形△OAB、△OBC、△OCD、△ODE、△OEF、△OFA 全等吗? 老师点评:(1)距离相等,(2)夹角相等,(3)前后图形全等,那么这个是否有一般性?下面请看这个实验. 请看我手里拿着的硬纸板,我在硬纸板上挖下一个三角形的洞,再挖一个点 O作为旋转中心,把挖好的硬纸板放在黑板上,先在黑板上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心 O 转动硬纸板,在黑板上再描出这个挖掉的三角形(△A′B′C′),移去硬纸板.(分组讨论)根据图回答下面问题(一组推荐一人上台说明) 1.线段 OA 与 OA′,OB 与 OB′,OC 与 OC′有什么关系? 2.∠AOA′,∠BOB′,∠COC′有什么关系? 3.△ABC 与△A′B′C′形状和大小有什么关系? 合作展示 1.如图,△ABC 绕 C 点旋转后,顶点 A 的对应点为点 D,试确定顶点 B对应点的位置,以及旋转后的三角形. 2.如图,四边形 ABCD 是边长为 1 的正方形,且 DE= 14,△ABF 是△ADE 的旋转图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)AF 的长度是多少?(4)如果连结 EF,那么△AEF 是怎样的三角形? 3 . 如 图 , 已 知 正 方 形 ABCD 的 对 角 线 交 于 O 点 , 若 点 E 在 AC 的 延 长 线上,AG⊥E...