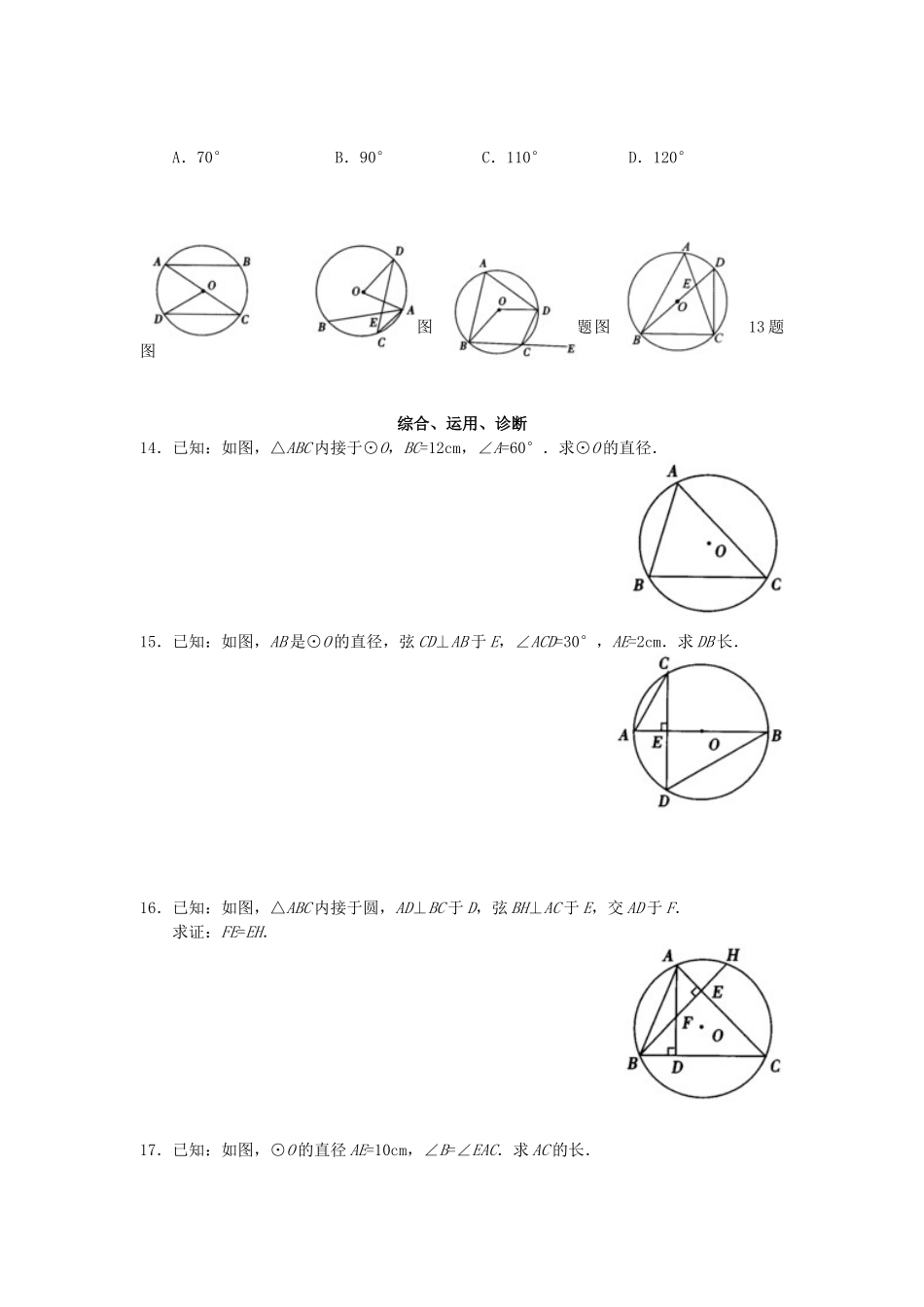
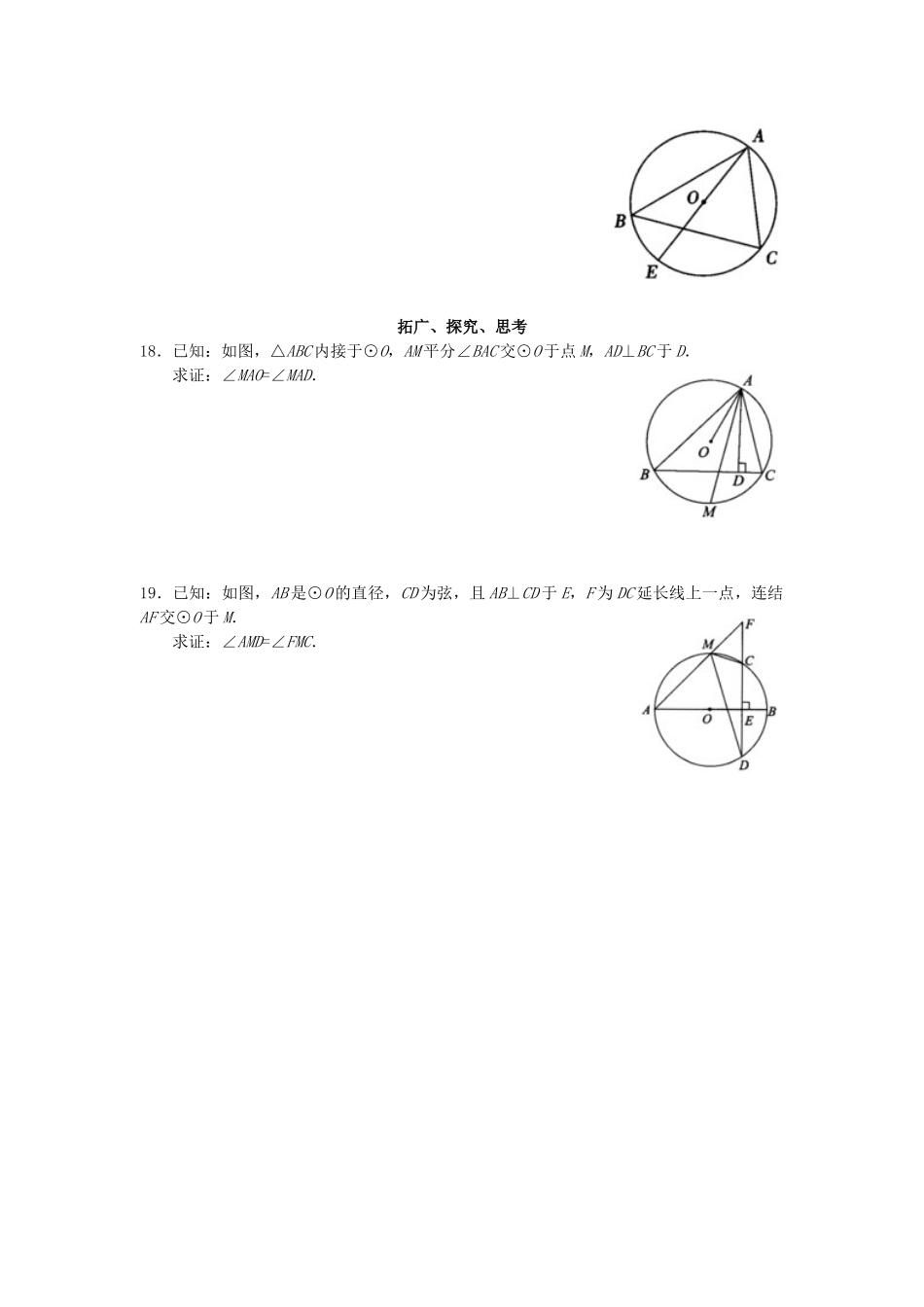
24.1.4 圆周角第 2 课时 圆内接四边形的性质及圆周角定理的综合运用学习要求1.理解圆周角的概念.2.掌握圆周角定理及其推论.3.理解圆内接四边形的性质,探究四点不共圆的性质.课堂学习检测一、基础知识填空1._________在圆上,并且角的两边都_________的角叫做圆周角.2.在同一圆中,一条弧所对的圆周角等于_________圆心角的_________.3.在同圆或等圆中,____________所对的圆周角____________.4._________所对的圆周角是直角.90°的圆周角______是直径.5 . 如 图 , 若 五 边 形ABCDE是 ⊙ O的 内 接 正 五 边 形 , 则∠BOC=______,∠ABE=______,∠ADC=______,∠ABC=______.6 . 如 图 , 若 六 边 形ABCDEF是 ⊙ O的 内 接 正 六 边 形 , 则∠AED=______,∠FAE=______,∠DAB=______,∠EFA=______.7.如图,ΔABC 是⊙O 的内接正三角形,若 P 是上一点,则∠BPC=______;若 M 是上一点,则∠BMC=______. 5 题图 6 题图 7 题图二、选择题8.在⊙O 中,若圆心角∠AOB=100°,C 是上一点,则∠ACB 等于( ).A.80°B.100°C.130°D.140°9.在圆中,弦 AB,CD 相交于 E.若∠ADC=46°,∠BCD=33°,则∠DEB 等于( ).A.13°B.79°C.38.5°D.101°10.如图,AC 是⊙O 的直径,弦 AB∥CD,若∠BAC=32°,则∠AOD 等于( ).A.64°B.48°C.32°D.76°11.如图,弦 AB,CD 相交于 E 点,若∠BAC=27°,∠BEC=64°,则∠AOD 等于( ).A.37°B.74°C.54°D.64°12.如图,四边形 ABCD 内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE 等于( ). A.69°B.42°C.48°D.38° 13.如图,△ABC 内接于⊙O,∠A=50°,∠ABC=60°,BD 是⊙O 的直径,BD 交 AC 于点 E,连结 DC,则∠AEB 等于( ).A.70°B.90°C.110°D.120° 10 题图 11 题图 12 题图 13 题图综合、运用、诊断14.已知:如图,△ABC 内接于⊙O,BC=12cm,∠A=60°.求⊙O 的直径.15.已知:如图,AB 是⊙O 的直径,弦 CD⊥AB 于 E,∠ACD=30°,AE=2cm.求 DB 长.16.已知:如图,△ABC 内接于圆,AD⊥BC 于 D,弦 BH⊥AC 于 E,交 AD 于 F.求证:FE=EH.17.已知:如图,⊙O 的直径 AE=10cm,∠B=∠EAC.求 AC 的长.拓广、探究、思考18.已知:如图,△ABC 内接于⊙O,AM 平分∠BAC 交⊙O 于点 M,AD⊥BC 于 D.求证:∠MAO=∠MAD.19.已知:如图,AB 是⊙O 的直径,CD 为弦,且 AB⊥CD 于 E,F 为 DC 延长线上一点,连结AF 交⊙O 于 M.求证:∠AMD=∠FMC.