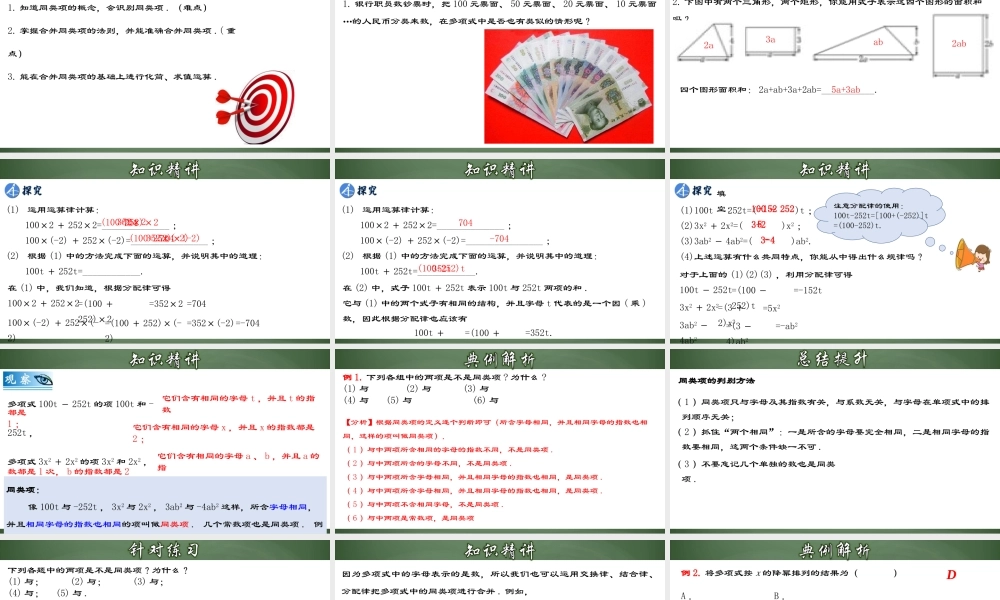
合并同类项1. 知道同类项的概念,会识别同类项 . (难点)2. 掌握合并同类项的法则,并能准确合并同类项 .( 重点)3. 能在合并同类项的基础上进行化简、求值运算 .1. 银行职员数钞票时,把 100 元票面、 50 元票面、 20 元票面、 10 元票面…的人民币分类来数,在多项式中是否也有类似的情形呢?2. 下图中有两个三角形,两个矩形,你能用式子表示这四个图形的面积和吗?四个图形面积和: 2a+ab+3a+2ab=___________.2a3aab2ab5a+3ab(1) 运用运算律计算: 100×2 + 252×2=______________ ; 100×(-2) + 252×(-2)=________________ ;(2) 根据 (1) 中的方法完成下面的运算,并说明其中的道理: 100t + 252t=____________.(100+252)×2(100+252)×(-2)在 (1) 中,我们知道,根据分配律可得 100×2 + 252×2352×2704352×(-2)-704=(100 +252)×2 =352×2100×(-2) + 252×(-2)=704=(100 + 252)×(-2)=352×(-2)=-704(1) 运用运算律计算: 100×2 + 252×2=______________ ; 100×(-2) + 252×(-2)=________________ ;(2) 根据 (1) 中的方法完成下面的运算,并说明其中的道理: 100t + 252t=____________.(100+252)t在 (2) 中,式子 100t + 252t 表示 100t 与 252t 两项的和 .它与 (1) 中的两个式子有相同的结构,并且字母 t 代表的是一个因 ( 乘 )数,因此根据分配律也应该有704-704100t +252t=(100 +252)t=352t.352t(1)100t - 252t=( )t ;(2)3x2 + 2x2=( )x2 ;(3)3ab2 - 4ab2=( )ab2.(4)上述运算有什么共同特点,你能从中得出什么规律吗?对于上面的 (1)(2)(3) ,利用分配律可得100t - 252t填空:100 - 252-1523ab2 -4ab2=(100 -252)t=-152t3x2 + 2x2=(3 +2)x2=5x23+25=-ab2=(3 -4)ab23-4-注意分配律的使用:100t-252t=[100+(-252)]t=(100-252)t.多项式 100t - 252t 的项 100t 和 -252t ,多项式 3x2 + 2x2 的项 3x2 和 2x2 ,多项式 3ab2 - 4ab2 的项 3ab2 和 -4ab2 ,它们含有相同的字母 t ,并且 t 的指数它们含有相同的字母 a 、 b ,并且 a 的指都是1 ;它们含有相同的字母 x ,并且 x 的指数都是2 ;数都是 1 次, b 的指数都是 2次 .同类项: 像 100t 与 -252t , 3x2 与 2x2 , 3ab2 与 -4ab2 这样,所含字母相同,并且相同字母的指...