（2025秋季）新人教版七年级数学上册2.2.2 去括号 课件

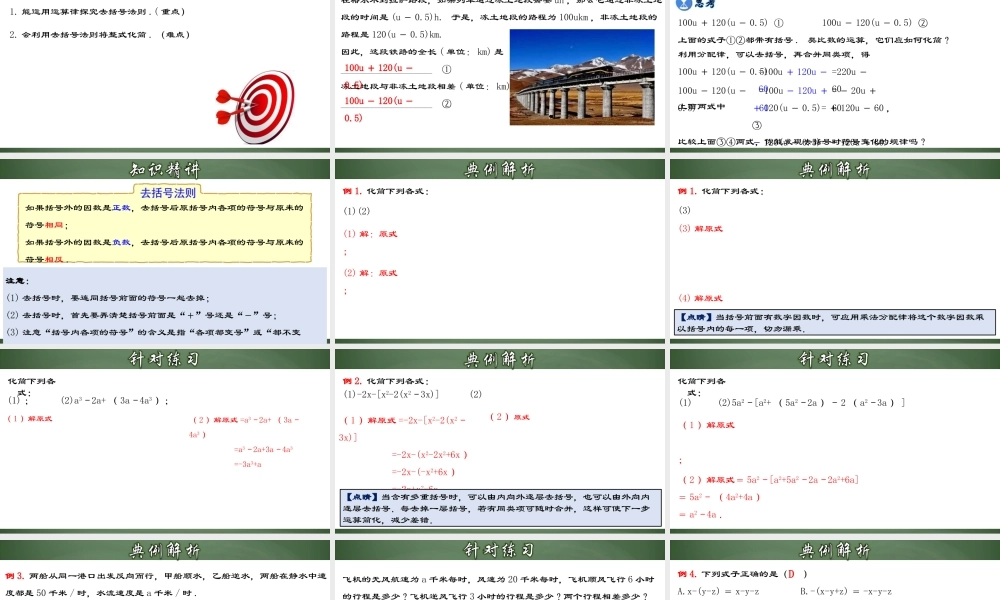
去 括 号1. 能运用运算律探究去括号法则 .( 重点）2. 会利用去括号法则将整式化简 . （难点）在格尔木到拉萨路段，如果列车通过冻土地段需要 uh ，那么它通过非冻土地段的时间是 (u － 0.5)h. 于是，冻土地段的路程为 100ukm ，非冻土地段的路程是 120(u － 0.5)km. 因此，这段铁路的全长 ( 单位： km) 是 ___________________ ①冻土地段与非冻土地段相差 ( 单位： km) ___________________ ②100u ＋ 120(u －0.5) 100u － 120(u －0.5) 100u ＋ 120(u － 0.5) ① 100u － 120(u － 0.5) ②上面的式子①②都带有括号 . 类比数的运算，它们应如何化简？利用分配律，可以去括号，再合并同类项，得100u ＋ 120(u － 0.5)=100u ＋ 120u －60100u － 120(u －0.5)=220u －60比较上面③④两式，你能发现去括号时符号变化的规律吗？=100u － 120u ＋60= － 20u ＋60上面两式中 ＋ 120(u － 0.5)= ＋ 120u － 60 ， ③－ 120(u － 0.5)= － 120u ＋ 60. ④如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反 .特别地，＋ (x － 3) 与－ (x － 3) 可以分别看作 1 与－ 1 分别乘 (x － 3). 利用分配律，可以将式子中的括号去掉，得 ＋ (x － 3)=x － 3 ，－ (x － 3)= － x ＋ 3.注意：(1) 去括号时，要连同括号前面的符号一起去掉；(2) 去括号时，首先要弄清楚括号前面是“＋”号还是“－”号；(3) 注意“括号内各项的符号”的含义是指“各项都变号”或“都不变号” .例 1. 化简下列各式：(1)(2)(1) 解：原式；(2) 解：原式；例 1. 化简下列各式：(3) (4) 解原式 (3) 解原式 【点睛】当括号前面有数字因数时，可应用乘法分配律将这个数字因数乘以括号内的每一项，切勿漏乘．(1) ； (2)a3﹣2a+ （ 3a﹣4a3 ）；（ 2 ）解原式 =a3﹣2a+ （ 3a﹣4a3 ） =a3﹣2a+3a﹣4a3 =-3a3+a化简下列各式：（ 1 ）解原式 例 2. 化简下列各式：(1)-2x-[x2-2(x2﹣3x)] (2)（ 1 ）解原式 =-2x-[x2-2(x2﹣3x)] =-2x-(x2-2x2+6x ） =-2x-(-x2+6x ） =-2x+x2-6x =x2-8x（ 2 ）原式【点睛】当含有多重括号时，可以由内向外逐层去括号，也可以由外向内逐层去括号．每去掉一层括号，若有同类项可随时合并，这样可使...