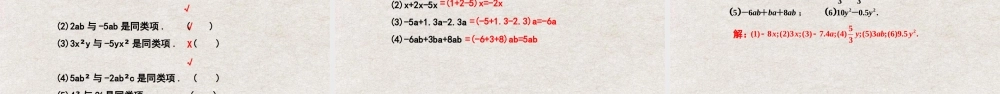第 2.2 整式的加减(第一课时合并同类项) 人教版数学七年级上册学习目标1. 知道同类项概念,会识别同类项;2. 掌握合并同类项的法则,并能准确合并同类项;3. 能在合并同类项的基础上进行化简求值、解决实际问题等 . 青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段 . 列车在冻土地段的行驶速度是 100km/h ,在非冻土地段的行驶速度可以达到 120km/h ,请根据这些数据回答下列问题: 在西宁到拉萨路段,列车通过非冻土地段所需时间是通过冻土地段所需时间的 2.1 倍,如果通过冻土地段需要 t 小时,能用含 t 的式子表示这段铁路的全长吗? 情境引入情境引入100t + 120×2.1t即: 100t +252t这个式子还能化简吗?互动新授探究(1) 运用有理数的运算律计算 : 100×2+252×2=_________, 100×(-2)+252×(-2)=_________; 100×2 + 252×2 100×(-2) + 252×(-2)=(100 +252)×2=352×2=(100 + 252)×(-2)=352×(-2)=704=-704704-704( 2 )根据 (1) 中的方法完成下面的运算,并说明其中的道理: 100t+252t=_________. 互动新授100t + 252t解:=(100 + 252)t=352t352t100×2 +252×2 =(100 +252)×2=352×2=(100 + 252)×(-2)=352×(-2)100×(-2) + 252×(-2)在 (1) 中,我们知道,根据分配律可得在 (2) 中,式子 100t+252t 表示 100t 与 252t 两项的和 . 式子 100t+252t 与 (1) 中的式子 100×2 + 252×2 和100×(-2) + 252×(-2)互动新授 有相同的结构,并且字母 t 代表的是一个因(乘)数,因此根据分配律也应该有 100t+252t=352t.互动新授探究 填空 :(1)100t-252t=( )t=( )t (2) 3x2+2x2=( )x2=( )x2 (3) 3ab2-4ab2=( )ab2=( )ab2上述运算有什么共同特点,你能从中得出什么规律?100-2523+23-4-152 5-1(1) 中多项式的项 100t 和 -252t 都含有相同的字母 t ,并且 t 的指数都是 1.(2) 中多项式的项 3x2 和 2x2 都含有相同的字母 x ,并且 x 的指数都是 2.(3) 中多项式的项 3ab2 和 -4ab2 都含有相同的字母 a,b ,并且 a 的指数都是 1,b 的指数都是 2.这些项可以叫做什么呢?互动新授同类项:像 3ab2 与 -4ab2 这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项 .几个常数项也是同类项 .例如: 4x2+2x+7+3x-8x2-2 =4x2-8x2+2x+3x+7-2 ( 交换律 )=(4x2-8x2)+(2x+3x)+(7-2)...