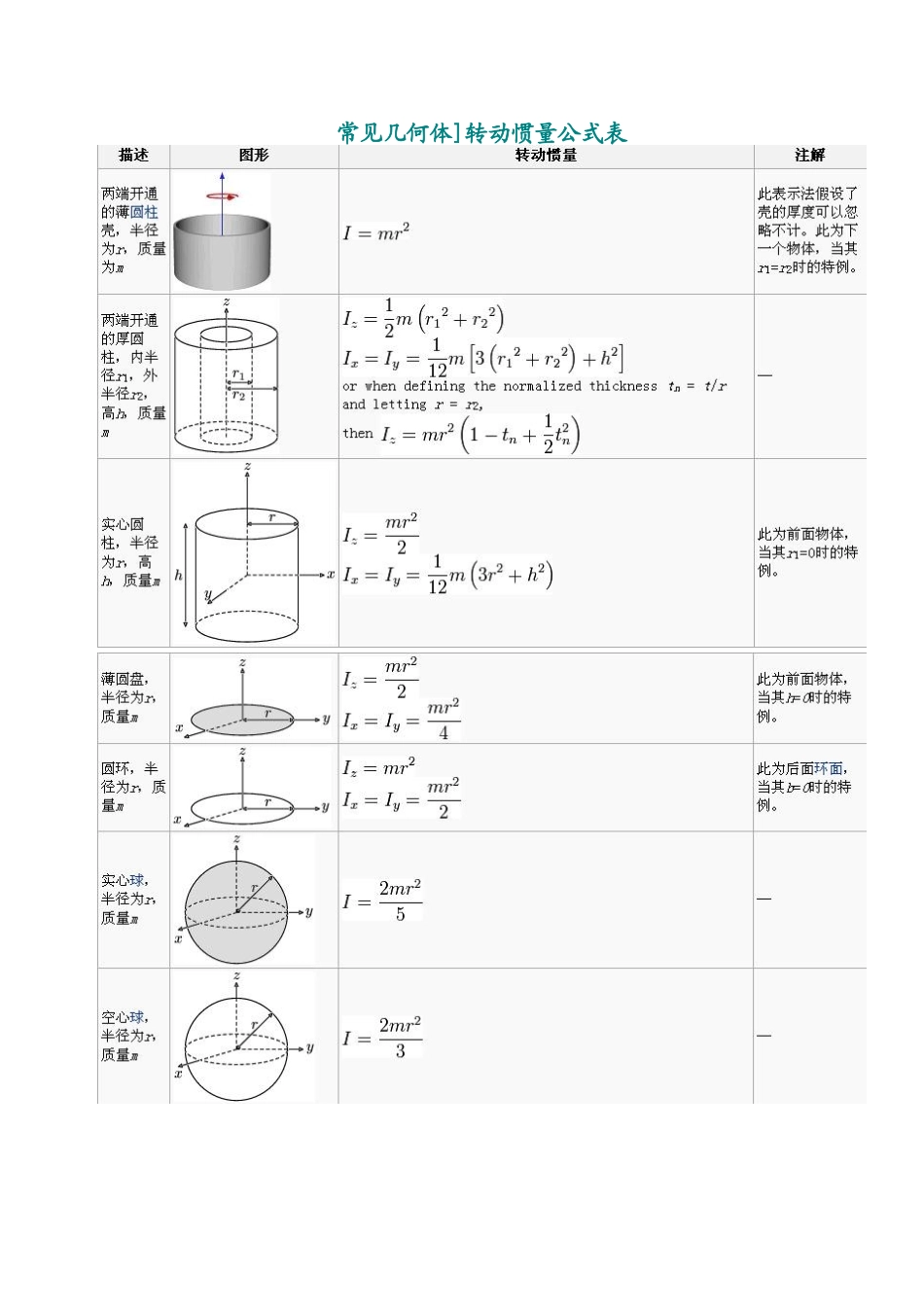
常见几何体]转动惯量公式表对于细杆当回转轴过杆得中点并垂直于杆时;J=m(L^2)/12其中 m 就是杆得质量,L 就是杆得长度。当回转轴过杆得端点并垂直于杆时:J=m(L^2)/3其中 m 就是杆得质量,L 就是杆得长度。对于圆柱体当回转轴就是圆柱体轴线时;J=m(r^2)/2其中 m 就是圆柱体得质量,r 就是圆柱体得半径。对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R 为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=1/2mR^2;﹙﹚当回转轴通过边缘与盘面垂直时,J=3/2mR^2;﹙﹚R 为其半径对于空心圆柱当回转轴为对称轴时,J=1/2m[(R1)^2+(R2)^2];﹙﹚R1 与 R2 分别为其内外半径。对于球壳当回转轴为中心轴时,J=2/3mR^2;﹙﹚当回转轴为球壳得切线时,J=5/3mR^2;﹙﹚R 为球壳半径。对于实心球体当回转轴为球体得中心轴时,J=2/5mR^2;﹙﹚当回转轴为球体得切线时,J=7/5mR^2;﹙﹚R 为球体半径对于立方体当回转轴为其中心轴时,J=1/6mL^2;﹙﹚当回转轴为其棱边时,J=2/3mL^2;﹙﹚当回转轴为其体对角线时,J=(3/16)mL^2;L 为立方体边长。只知道转动惯量得计算方式而不能使用就是没有意义得。下面给出一些(绕定轴转动时)得刚体动力学公式。角加速度与合外力矩得关系:角加速度与合外力矩式中 M 为合外力矩,β 为角加速度。可以瞧出这个式子与牛顿第二定律就是对应得。角动量:角动量刚体得定轴转动动能:转动动能注意这只就是刚体绕定轴得转动动能,其总动能应该再加上质心动能。只用 E=(1/2)mv^2 不好分析转动刚体得问题,就是因为其中不包含刚体得任何转动信息,里面得速度 v 只代表刚体得质心运动情况。由这一公式,可以从能量得角度分析刚体动力学得问题。转动惯量(Moment of Inertia)就是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止得特性)得量度,用字母 I 或 J 表示。其量值取决于物体得形状、质量分布及转轴得位置。转动惯量只决定于刚体得形状、质量分布与转轴得位置,而同刚体绕轴得转动状态(如角速度得大小)无关。形状规则得匀质刚体,其转动惯量可直接用公式计算得到。而对于不规则刚体或非均质刚体得转动惯量,一般通过实验得方法来进行测定,因而实验方法就显得十分重要。转动惯量得表达式为 I=∑ mi*ri^2,若刚体得质量就是连续分布得,则转动惯量得计算公式可写成 I=∫r^2dm=∫r^2ρdV(式中 mi 表示刚体得某个质元得质量,ri 表示该质元到转轴得垂直距离,ρ 表示该处得密度,求与号(或积...