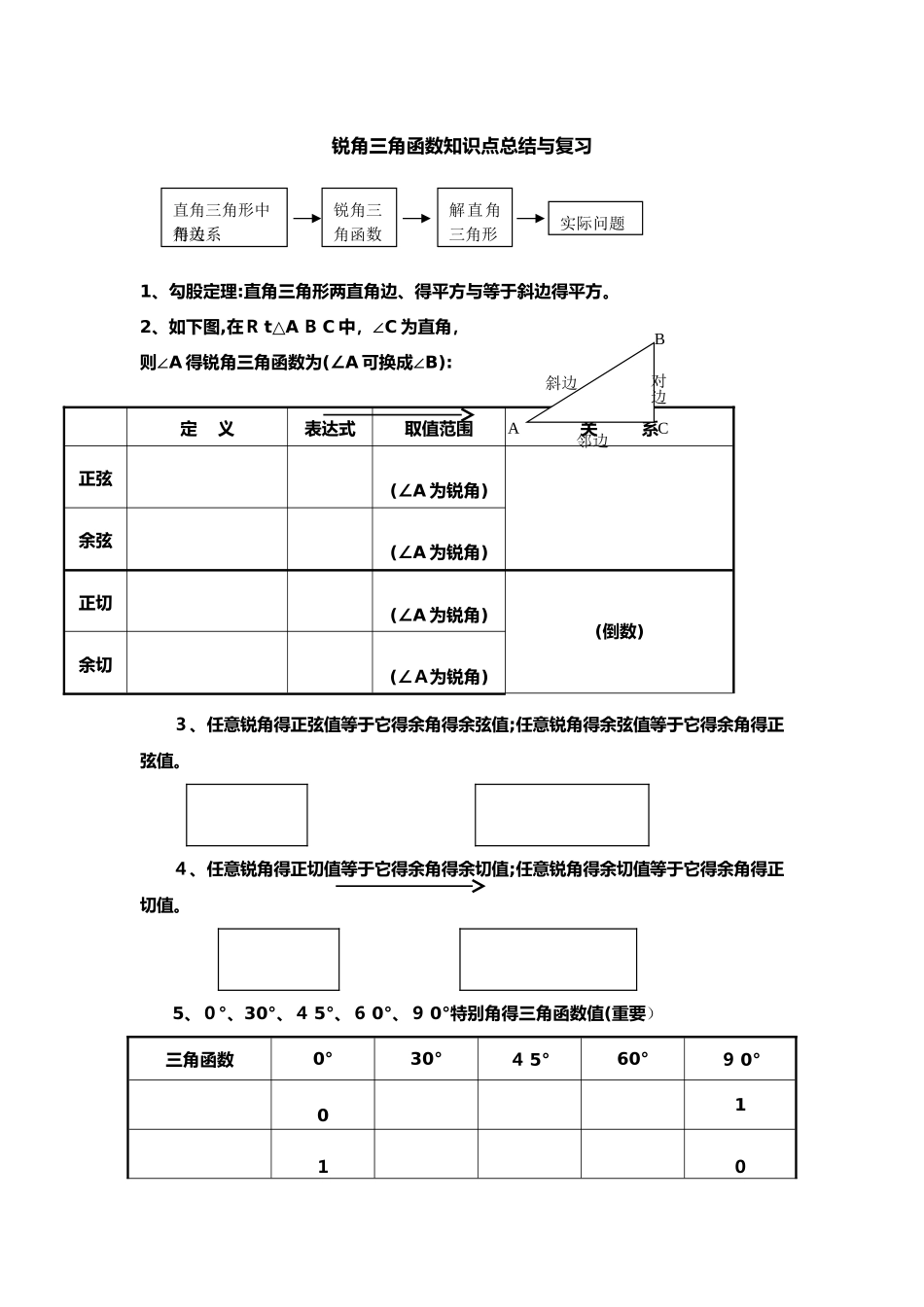
锐角三角函数知识点总结与复习1、勾股定理:直角三角形两直角边、得平方与等于斜边得平方。 2、如下图,在R t△A B C 中,∠C 为直角,则∠A 得锐角三角函数为(∠A 可换成∠B):3、任意锐角得正弦值等于它得余角得余弦值;任意锐角得余弦值等于它得余角得正弦值。 4、任意锐角得正切值等于它得余角得余切值;任意锐角得余切值等于它得余角得正切值。 5、0°、30°、4 5°、6 0°、9 0°特别角得三角函数值(重要)三角函数0°30°4 5°60°9 0°0110定 义表达式取值范围关 系正弦(∠A 为锐角)余弦(∠A 为锐角)正切(∠A 为锐角) (倒数)余切(∠A为锐角) 对边邻边斜边ACB 直角三角形中得边角关系锐角三角函数解直角三角形实际问题01不存在不存在10 6、正弦、余弦得增减性: 当 0°≤≤90°时,sin随得增大而增大,cos 随得增大而减小。7、正切、余切得增减性:当0°<<90°时,t an随得增大而增大,cot 随得增大而减小。一、知识性专题专题 1:锐角三角函数得定义 例 1 在R t△ABC 中,∠A CB=90°,B C=1,AB=2,则下列结论正确得就就是 ( )A、si n A= B、tan A= C、cos B= D、t a n B= 分析 sin A==,t an A==,co s B==、故选 D、 例 2 在△A BC 中,∠C=9 0°,c osA=,则 tan A 等于 ; 分析 在 Rt△ABC 中,设 A C=3 k,AB=5 k,则 BC=4k,由定义可知t an A=、分析 在 Rt△ABC 中,BC==3,∴sin A=、故填、例 3(12·哈尔滨)在 R t△A B C 中,∠C=9 0 0,AC=4,A B=5,则sinB 得值就就是 ;【解析】本题考查了锐角三角函数得意义、解题思路:在直角三角形中,锐角得正弦等于对边比邻边,故s inB=、例 4(2 0 1 2内江)如图 4 所示,△A B C 得顶点就就是正方形网格得格点,则 sinA得值为 ;ﻩ【解析】欲求 s in A,需先寻找∠A 所在得直角三角形,而图形中∠A 所在得△ABC 并不就就是直角三角形,所以需要作高、观察格点图形发现连接CD(如下图所示),恰好可证得 C D⊥AB,于就就是有 sinA===、例 5 ( 2025 宁波),Rt△ABC,∠C=900,AB=6,cosB=,则B C 得长为 ;【解析】cos B==,又 A B=6∴BC=4例 6(2025 贵州铜仁)如图,定义:在直角三角形 ABC 中,锐角得邻边与对边得比叫做角得余切,记作 c t a n, 即 ctan=,根据上述角得余切定义,解下列问题:...