高一数学上 2.4《截距法解线性规划问题》素材 沪教版

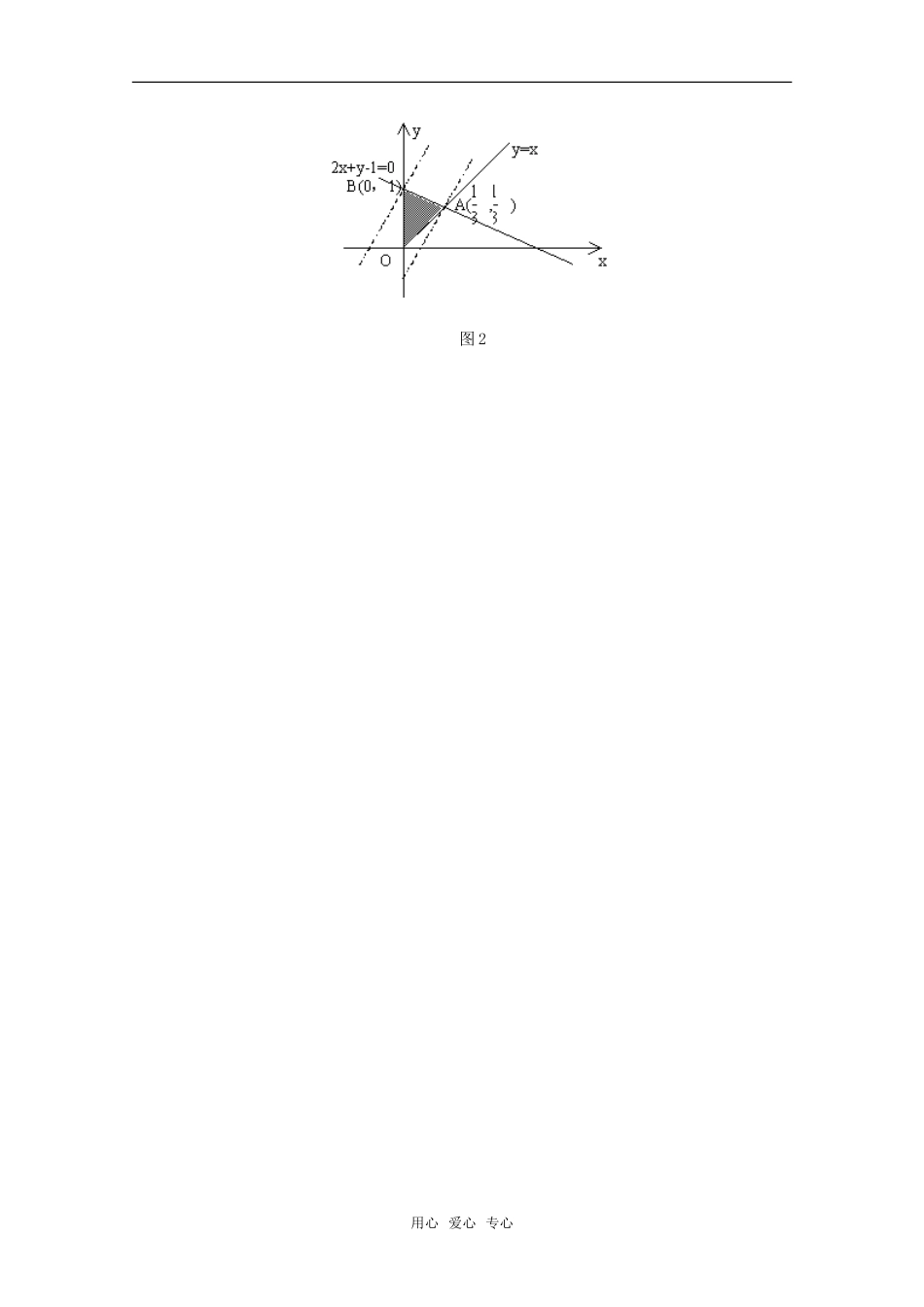
[截距法]解线性规划问题由于线性规划的目标函数：zaxby b()0 可变形为 yabxzb，则 zb为直线 yabxzb的纵截距，那么我们在用线性规划求最值时便可以得到如下结论：（1）当b  0 时，直线 yabxzb所经过可行域上的点使其纵截距最大时，便是 z 取得最大值的点；反之，使纵截距取得最小值的点，就是 z 取得最小值的点。（2）当b  0 时，与b  0 时情形正好相反，直线 yabxzb所经过可行域上的点使其纵截距最大时，是 z 取得最小值的点；使纵截距取得最小值的点，便是 z 取得最大值的点。例 1. 设 x，y 满足约束条件xyyxy10,,,求 zxy2的最大值、最小值。解：如图 1 作出可行域，目标函数 zxy2表示直线 yxz2在 y 轴上的截距，可见当直线过 A（1，0）时，截距值最大zmax   2102 ，当直线过点 O（0，0）时，截距值最小zmin 0 。图 1例 2. 设 x y,满足约束条件xxyxy021,,, 求 zxy32的最大值和最小值。解：如图 2 作出可行域，因为由图 2 可知过点 B 时纵截距最大，zxy32取得最小值，所以 zmin    30212 ； 过 点 A 时 纵 截 距 最 小 ， z 在 A （ 1313,） 处 取 最 大 值 ，zmax   31321313。用心 爱心 专心图 2用心 爱心 专心