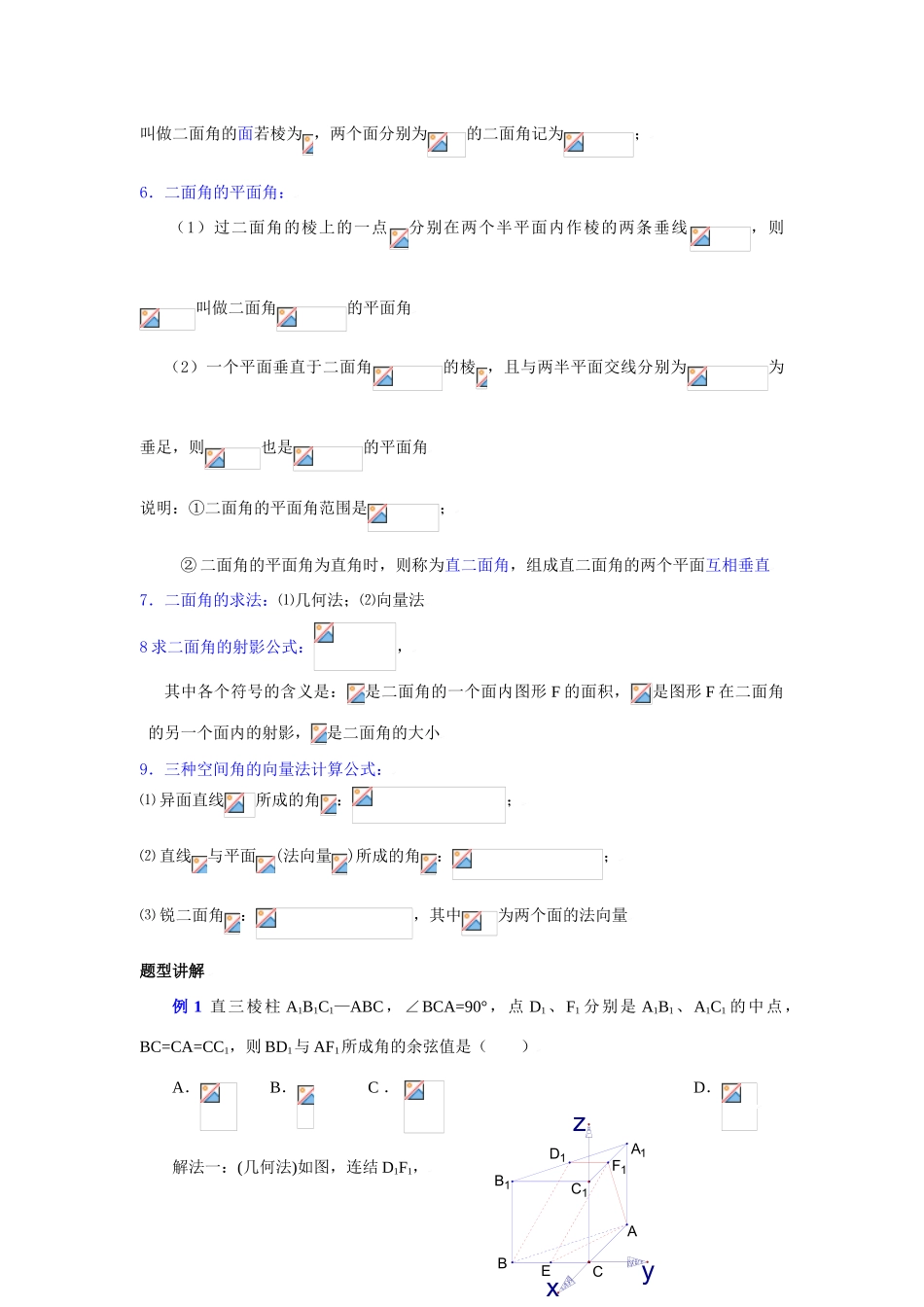
DCOAB题目 第九章(B)直线、平面、简单几何体空间角高考要求 1 掌握直线和直线、直线和平面、平面和平面所成的角的概念 2 会求直线和直线、直线和平面、平面和平面所成的角知识点归纳 1.异面直线所成的角:已知两条异面直线,经过空间任一点作直线,所成的角的大小与点的选择无关,把所成的锐角(或直角)叫异面直线所成的角(或夹角).为了简便,点通常取在异面直线的一条上异面直线所成的角的范围:2.求异面直线所成的角的方法:(1)几何法;(2)向量法3.直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角一直线垂直于平面,所成的角是直角一直线平行于平面或在平面内,所成角为 0角直线和平面所成角范围: 0,(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角4.公式:平面的斜线 a 与内一直线 b 相交成 θ 角,且 a 与相交成1 角,a 在上的射影 c 与 b 相交成2角,则有5 二面角:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面21cbaPOAB叫做二面角的面若棱为 ,两个面分别为的二面角记为;6.二面角的平面角: (1)过二面角的棱上的一点分别在两个半平面内作棱的两条垂线,则叫做二面角的平面角(2)一个平面垂直于二面角的棱 ,且与两半平面交线分别为为垂足,则也是的平面角说明:①二面角的平面角范围是;② 二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直7.二面角的求法:⑴几何法;⑵向量法8 求二面角的射影公式:,其中各个符号的含义是:是二面角的一个面内图形 F 的面积,是图形 F 在二面角的另一个面内的射影,是二面角的大小9.三种空间角的向量法计算公式:⑴ 异面直线所成的角:;⑵ 直线与平面(法向量)所成的角:;⑶ 锐二面角:,其中为两个面的法向量题型讲解 例 1 直三棱柱 A1B1C1—ABC,∠BCA=90°,点 D1、F1 分别是 A1B1、A1C1 的中点,BC=CA=CC1,则 BD1与 AF1所成角的余弦值是( )A. B. C . D.解法一:(几何法)如图,连结 D1F1,ABCA1B1C1D1EF1xzy则 D1F1 BC ∴D1F1 设点 E 为 BC 中点∴D1F1 BE EF1∴∠EF1A 或补角即为所求由余弦定理可求得 cos∠EF1A=.解法二:(向量法)建立...