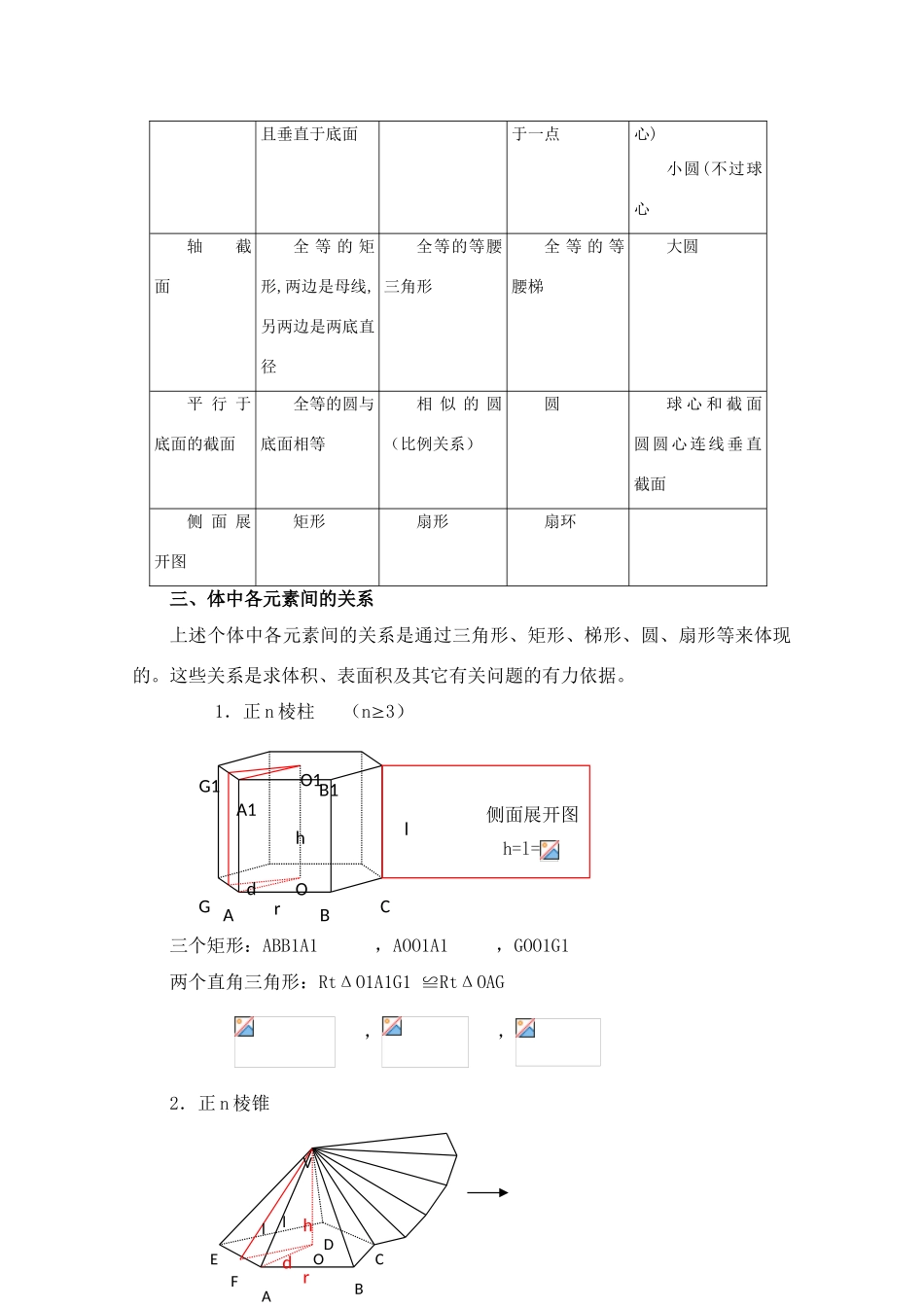
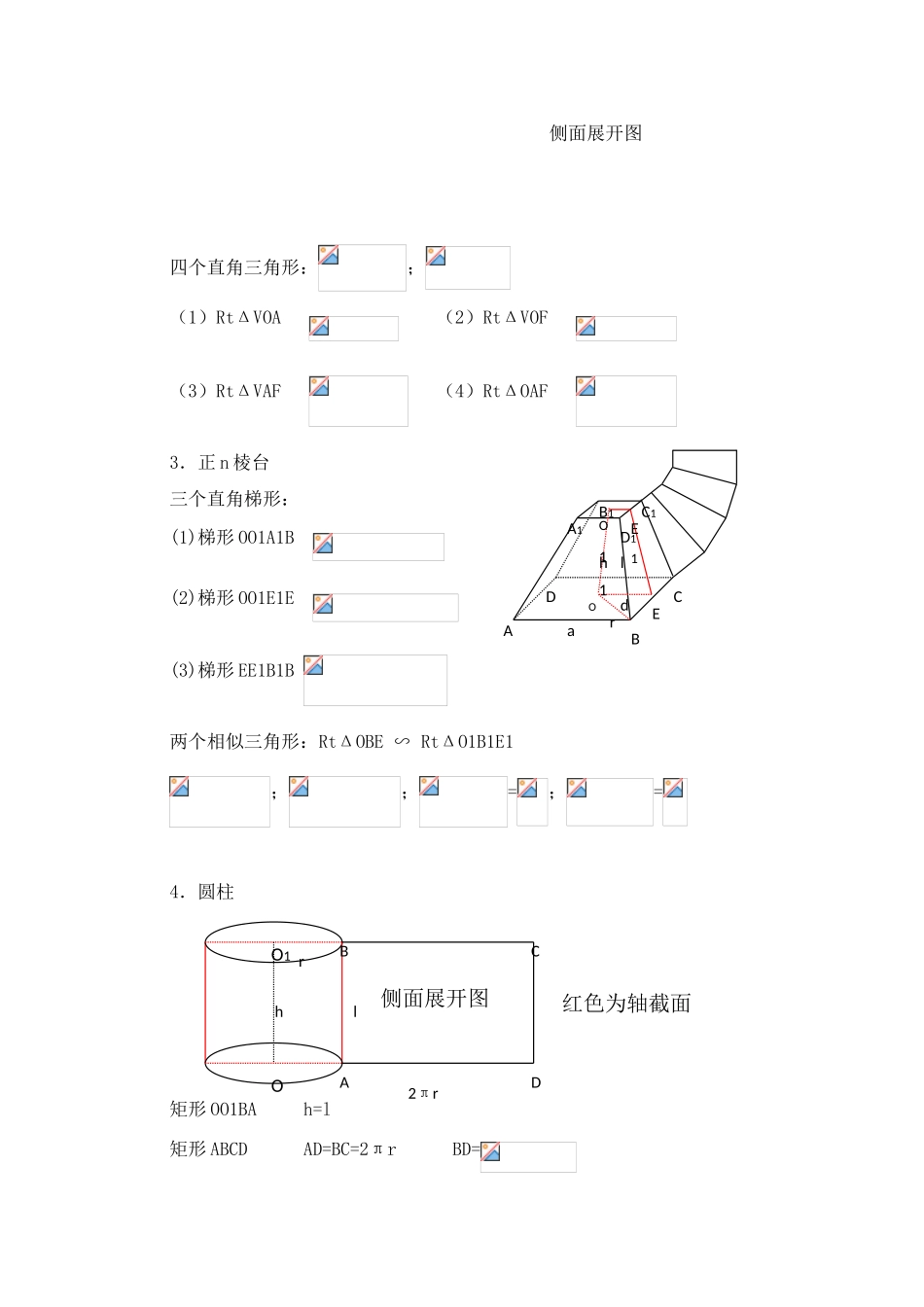
第二节 旋转体的概念和性质一. 旋转体定义:一条平面曲线(包括直线)绕它所在的平面内的一条定直线旋转所形成的曲面叫旋转面。这线叫旋转轴。无论旋转到什麽位置这条曲线叫旋转面的母线。封闭的旋转面围成的几何体叫旋转体。旋转面的轴叫旋转体的轴。二. 几种常见的旋转体定义:矩形绕一边旋转一周所围成的几何体叫圆柱。 绕一直角边旋转一周所围成的几何体叫圆锥。 直角梯形绕垂直于底边的腰旋转一周所围成的几何体叫圆台 圆绕它的直径旋转一周所围成的几何体叫球。注意:(1)垂直于轴的线段绕轴旋转一周形成圆面。 (2)与轴相交的直线绕轴旋转一周形成圆锥面。 (3)与轴平行的直线绕轴旋转一周形成圆柱面。 (4)不平行也不相交的线段绕轴旋转一周形成圆台面。折线旋转形成 上锥、下台2.性质圆 柱圆 锥圆 台球底 面平行且全等的圆圆 面相 似 的 两个圆面轴 线过底面圆心且垂直底面过顶点和底面圆心垂直于底面过 上 下 底面 圆 心 且 垂 直底面过球心母 线平行且相等相交于一点延 长 线 交大 圆 ( 过 球OOOO1O1A1A1VAAA且垂直于底面于一点心)小圆(不过球心轴 截 面全 等 的 矩形,两边是母线,另两边是两底直径全等的等腰三角形全 等 的 等腰梯大圆平 行 于底面的截面全等的圆与底面相等相 似 的 圆(比例关系)圆球 心 和 截 面圆圆心连线垂直截面侧 面 展开图矩形扇形扇环三、体中各元素间的关系上述个体中各元素间的关系是通过三角形、矩形、梯形、圆、扇形等来体现的。这些关系是求体积、表面积及其它有关问题的有力依据。高·考¥资%源~网1.正 n 棱柱 (n3) 侧面展开图 h=l=三个矩形:ABB1A1 ,AOO1A1 ,GOO1G1 两个直角三角形:RtΔO1A1G1 ≌RtΔOAG , ,2.正 n 棱锥 rdG ABChB1G1A1O1OlFABrdEOCDVhll 侧面展开图四个直角三角形:;(1)RtΔVOA (2)RtΔVOF (3)RtΔVAF (4)RtΔOAF 3.正 n 棱台三个直角梯形:(1)梯形 OO1A1B (2)梯形 OO1E1E (3)梯形 EE1B1B 两个相似三角形:RtΔOBE ∽ RtΔO1B1E1;;=;=4.圆柱矩形 OO1BA h=l矩形 ABCD AD=BC=2πr BD=DC1A1D1CBAadrEh lB1E1OO11ADCBl hO1Or侧面展开图2πr红色为轴截面S 圆柱侧=S 矩 ABCD=2πrl BD 是从 B 绕圆柱侧面一周到 A 的最短距离5.圆锥: 一个三角形及一个扇形RtΔOPA 中 扇形中 =C=2πr ;θ= ;=2lsin为从 A 出发绕圆锥侧面一周再回到 A 的...