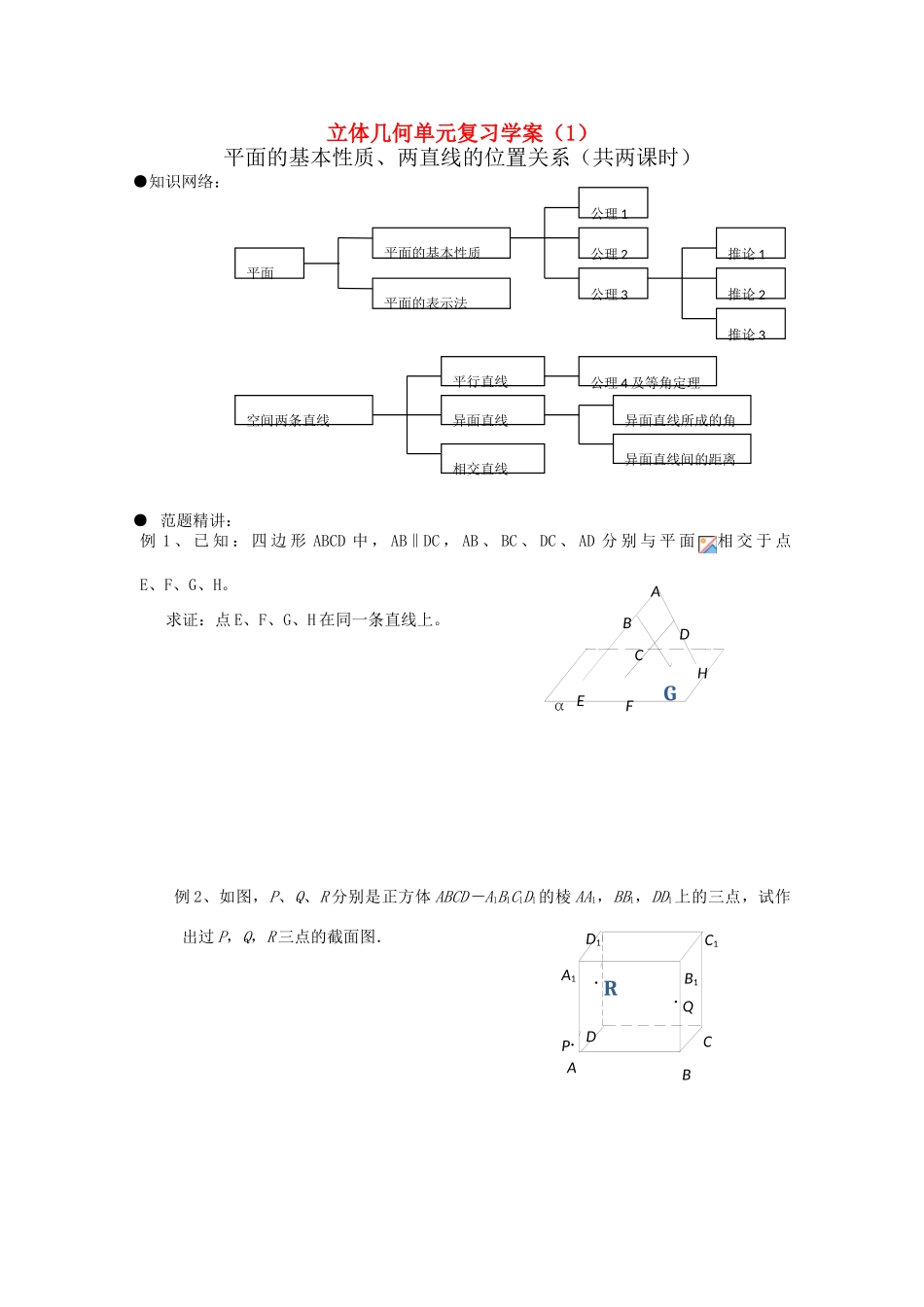
立体几何单元复习学案(1)平面的基本性质、两直线的位置关系(共两课时)●知识网络: ● 范题精讲:例 1 、 已 知 : 四 边 形 ABCD 中 , AB‖DC , AB 、 BC 、 DC 、 AD 分 别 与 平 面相 交 于 点E、F、G、H。求证:点 E、F、G、H 在同一条直线上。 例 2、如图,P、Q、R 分别是正方体 ABCD-A1B1C1D1的棱 AA1,BB1,DD1上的三点,试作出过 P,Q,R 三点的截面图.平面平面的基本性质平面的表示法公理 1公理 2公理 3推论 1推论 2推论 3空间两条直线平行直线异面直线相交直线公理 4 及等角定理异面直线所成的角异面直线间的距离αDCBAEFHGA1ABB1DD1CC1RQP···例 3、已知平面四边形 EFGH 的四个顶点分别在空间四边形 ABCD 的四条边上,求证:直线 EH 与 FG 相交,则它们的交点必在直线 BD 上。例 4 、 已 知 不 共 面 的 三 条 直 线、、相 交 于 点,,,,,求证:与是异面直线.例 5、如图,在正方体 ABCD-A1B1C1D1中,E 是 B1C1的中点,O 是正方形 A1B1C1D1的中心,连接AO,CE,求异面直线 AO 与 CE 所成的角的余弦。ACDC1D1A1B1EO●配套练习卷:平面的基本性质,两直线的位置关系YCY本试卷分第Ⅰ卷和第Ⅱ卷两部分.共 150 分.第Ⅰ卷(选择题)一、选择题1.若直线上有两个点在平面外,则 ( )A.直线上至少有一个点在平面内 B.直线上有无穷多个点在平面内C.直线上所有点都在平面外D.直线上至多有一个点在平面内2.在空间中,下列命题正确的是 ( )A.对边相等的四边形一定是平面图形 B.四边相等的四边形一定是平面图形C.有一组对边平行且相等的四边形是平面图形 D.有一组对角相等的四边形是平面图形3.在空间四点中,无三点共线是四点共面的 ( )A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件4.两条异面直线所成的角为 θ,则 θ 的取值范围是 ( )A B C D 5.如图:正四面体 S-ABC 中,如果 E,F 分别是 SC,AB 的中点,那么异面直线 EF 与 SA 所成的角等于 ( )A.90° B.45°C.60° D.30°6.一条直线与两条平行线中的一条是异面直线,那么它与另一条直线的位置关系是( )A.相交 B.异面 C.平行 D.相交或异面7.异面直线 a、b 成 60°,直线 c⊥a,则直线 b 与 c 所成的角的范围为 ( )A.[30°,90°] B.[60°,90°] C.[30°,60...