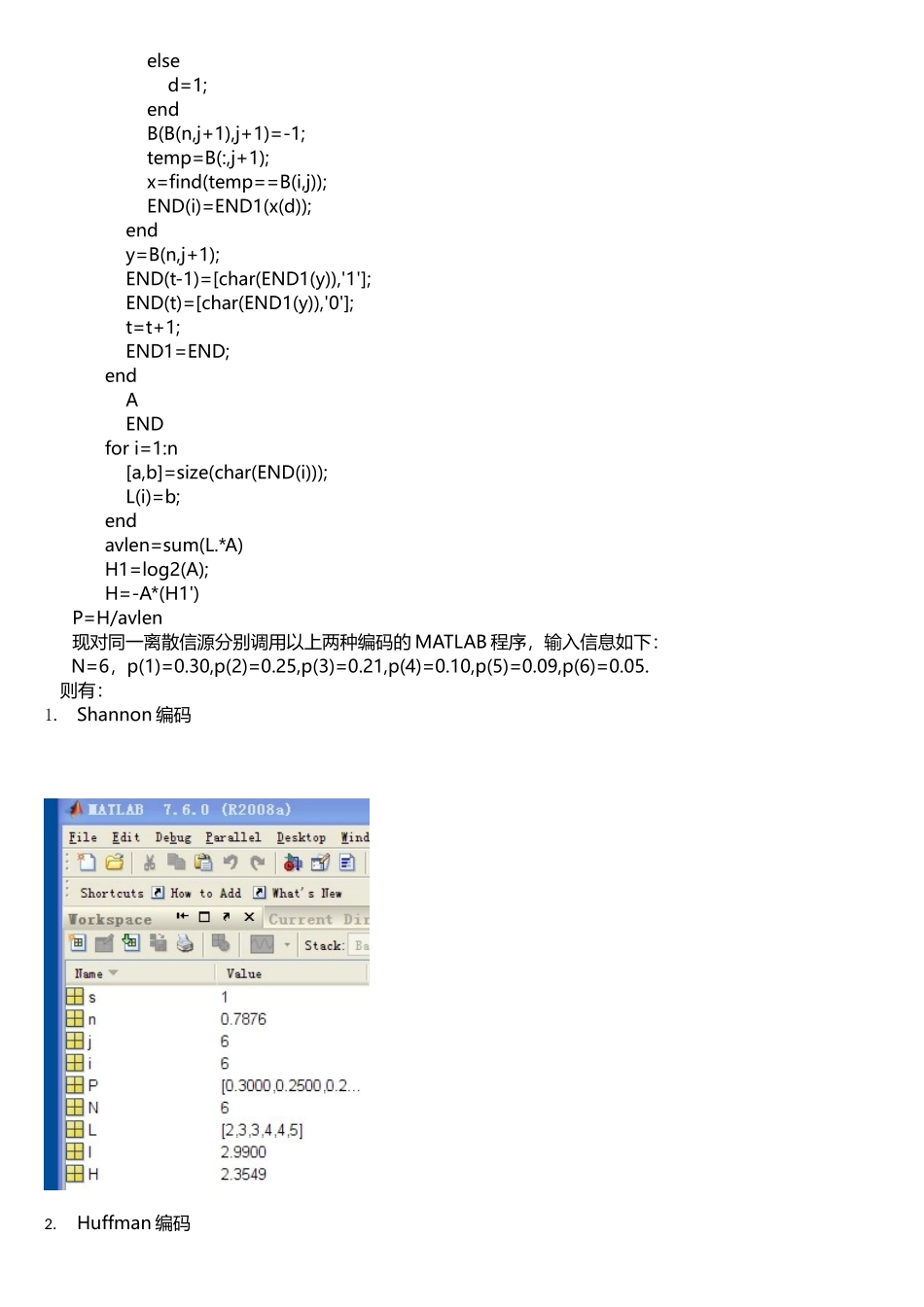
无失真变长编码及其 MATLAB 实现 我最近阅读了一篇关于无失真变长编码的期刊文献,通过阅读这篇文章我学到了更多关于信源编码的知识以及几种编码方法的 MATLAB 实现过程。这篇文章主要介绍了无失真变长编码的两种编码方法:Shannon 和 Huffman 编码,以及它们的MATLAB 实现方法和分析比较。我们都知道通信的本质就是信息的传输,即信源信息通过信道传给信宿,关键就是要高质量、高速度地传送信息,为了提高信号的传输速率,主要必须解决信号失真和受干扰这两个问题。文章针对无失真这种情况讲述了两种无失真编码的原理,即 Shannon 编码和 Huffman 编码,因为这两种编码方法的工作量很大,若采纳人工计算就会使工作效率和编码精确度大大降低,因而运用了语言简洁方便的 MATLAB 编程软件来实现其编码,并举出了两种编码方法的 MATLAB 实例及对两者进行了比较来说明两者的优缺点。无失真信源编码主要有等长编码和变长编码两种,其中等长编码的效率较低,而变长编码具有很高的效率,往往在码长不大时就可编出效率很高而且无失真的信源码,因此一般广泛采纳后者。变长编码中用编码效率来衡量各种编码方法的优劣,编码效率为:,其中:为信息熵,,为信源符号出现的概率;为平均码长,。对同一信源来说,若码的平均码长越短,越接近信息熵得值,则编码效率越接近 1,编码方法就越好。下面通过 MATLAB 实例来比较 Shannon 编码和 Huffman 编码。1.Shannon 编码方法及 MATLAB 实现:第一步:将信源发出的 N 个消息符号按其概率的递减次序依次排列。第二步:计算第 i 个消息的二进制代码组的码长。第三步:计算第 I 个消息的累加概率,然后将累加概率变换成二进制数。第四步:去除小数点,并根据码长,取小数点后位数作为第 i 个消息的代码组。MATLAB 实现:clear;N=input('N=');s=0;I=0;H=0;for i=1:NP(i)=input('P=');s=s+P(i);H=H+(-P(i)*log2(P(i)));endif abs(s-1)>0 error('不符合概率分布');endfor i=1:N-1for j=i+1:Nif P(i)