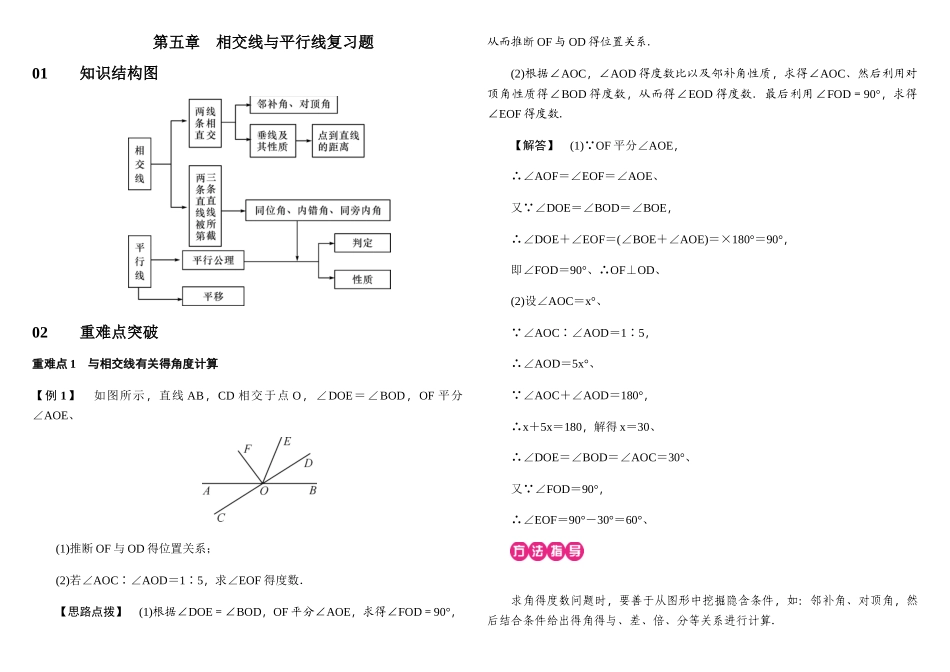
第五章 相交线与平行线复习题01 知识结构图02 重难点突破重难点 1 与相交线有关得角度计算【例 1】 如图所示，直线 AB，CD 相交于点 O，∠DOE＝∠BOD，OF 平分∠AOE、(1)推断 OF 与 OD 得位置关系；(2)若∠AOC∶∠AOD＝1∶5，求∠EOF 得度数．【思路点拨】 (1)根据∠DOE＝∠BOD，OF 平分∠AOE，求得∠FOD＝90°，从而推断 OF 与 OD 得位置关系．(2)根据∠AOC，∠AOD 得度数比以及邻补角性质，求得∠AOC、然后利用对顶角性质得∠BOD 得度数，从而得∠EOD 得度数．最后利用∠FOD＝90°，求得∠EOF 得度数．【解答】 (1) OF 平分∠AOE，∴∠AOF＝∠EOF＝∠AOE、又 ∠DOE＝∠BOD＝∠BOE，∴∠DOE＋∠EOF＝(∠BOE＋∠AOE)＝×180°＝90°，即∠FOD＝90°、∴OF⊥OD、(2)设∠AOC＝x°、 ∠AOC∶∠AOD＝1∶5，∴∠AOD＝5x°、 ∠AOC＋∠AOD＝180°，∴x＋5x＝180，解得 x＝30、∴∠DOE＝∠BOD＝∠AOC＝30°、又 ∠FOD＝90°，∴∠EOF＝90°－30°＝60°、求角得度数问题时，要善于从图形中挖掘隐含条件，如：邻补角、对顶角，然后结合条件给出得角得与、差、倍、分等关系进行计算．1．如图，直线 AB 与直线 CD 相交于点 O，MO⊥AB，垂足为 O、已知∠AOD＝136°，则∠COM 得度数为(C)A．36° B．44° C．46° D．54°2．如图，已知直线 AB 与 CD 交于点 O，ON 平分∠DOB、若∠BOC＝110°，则∠DON 为 35°．3．如图所示，O 就是直线 AB 上一点，∠AOC＝∠BOC，OC 就是∠AOD 得平分线．(1)求∠COD 得度数；(2)推断 OD 与 AB 得位置关系，并说出理由
