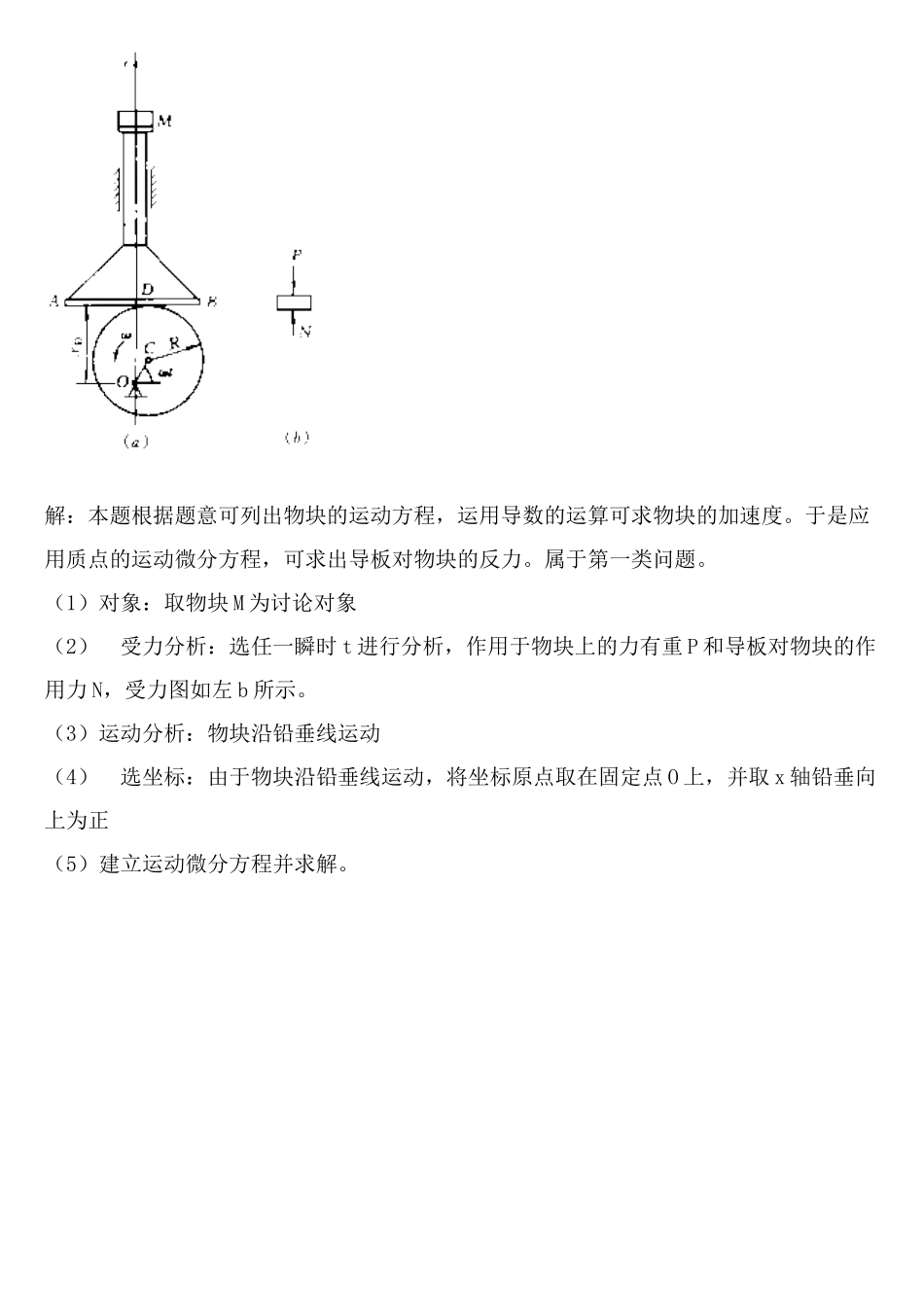
动力学基本定律和质点运动微分方程第二十九讲 动力学 一、内容提要:本讲主要讲述动力学基本定律和质点运动微分方程、动量定理、动量矩定理等内容。二、本讲的重点与难点是:动力学基本定律和质点运动微分方程、质点的动量定理、质点系的动量定理、质心运动定理、质点的动量矩定理、质点系的动量矩定理三、内容讲解: 1、 动力学基本定律和质点运动微分方程(一)动力学基本定律(通称牛顿三定律)第一定律:任何质点如不受力作用,则将保持其原来静止的或匀速直线运动的状态。这个定律说明了任何质点都具有保持静止或匀速直线运动状态的性质,质点保持这种运动状态不变的固有的属性称为惯性,所以这一定律也称为惯性定律。第二定律:质点受到力作用所产生的加速度其大小与力成正比,与质点的质量成反比,加速度的方向与力的方向相同。(三)质点动力学的两类基本问题第一类问题是:已知质点的运动,求作用于质点上的力。第二类问题是:已知作用于质点上的力,求质点的运动。在这类问题中,已知的作用力可以表现为各种形式,如可以是常力、变力、时间的函数、速度的函数、位置的函数以及同时是这些因素的函数等。解这类问题归结为解微分方程,即积分问题,积分时出现的积分常数由质点运动的初始条件(初始位置和初始速度)确定。只有当被积函数较简单时才能求得精确解。当被积函数关系复杂时,求解很困难只能求到近似解。下面举例来说明利用质点运动微分方程求解质点动力学的两类问题。例 1、如下图所示,半径为 R 的偏心轮绕 O 轴以匀角速度 ω 转动,推动导板 AB 沿铅垂轨道运动。已知偏心距 OC=e,开始时 OC 沿水平线。若在导板顶部放有一质量为 m 的物块M,求(1)物块对导板的最大反力及此时偏心 C 的位置(2)使物块不离开导板 ω 的最大值。解:本题根据题意可列出物块的运动方程,运用导数的运算可求物块的加速度。于是应用质点的运动微分方程,可求出导板对物块的反力。属于第一类问题。(1)对象:取物块 M 为讨论对象(2) 受力分析:选任一瞬时 t 进行分析,作用于物块上的力有重 P 和导板对物块的作用力 N,受力图如左 b 所示。(3)运动分析:物块沿铅垂线运动(4) 选坐标:由于物块沿铅垂线运动,将坐标原点取在固定点 O 上,并取 x 轴铅垂向上为正(5)建立运动微分方程并求解。