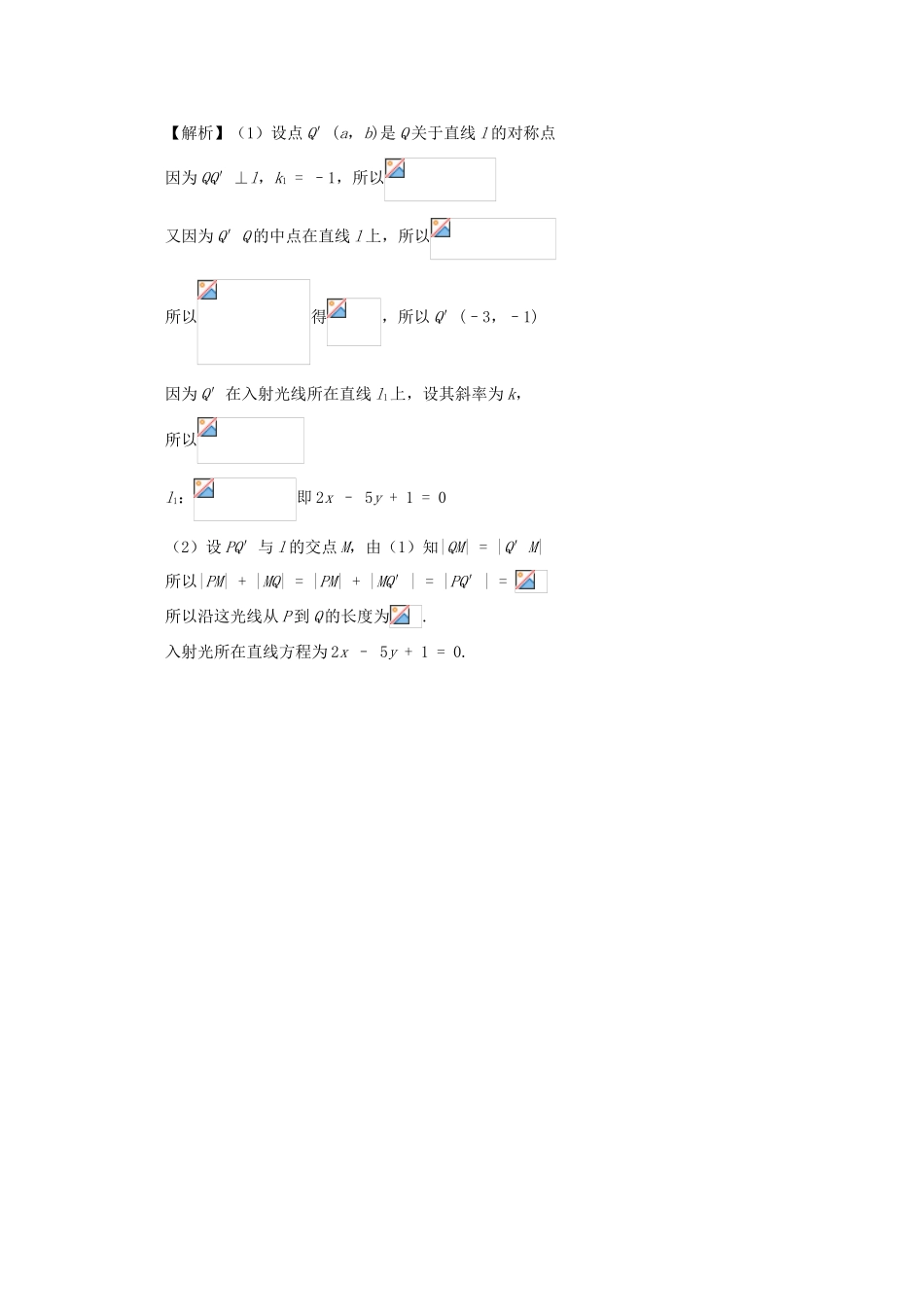
两点间的距离例 1 已知点 A (–1,2),在 x 轴上求一点,使|PA| = |PB|,并求|PA|的值.解:设所求点 P (x,0),于是有∴x2 + 2x + 5 = x2 – 4x + 11解得 x = 1∴所求点 P (1,0)且经典习题例 1 已知点 A(3,6),在 x 轴上的点 P 与点 A 的距离等于 10,求点 P 的坐标【解析】设点 P 的坐标为 (x,0),由|PA| = 10,得: 解得:x = 11 或 x = –5.所以点 P 的坐标为(–5,0)或(11,0).例 2 在直线 l:3x – y – 1 = 0 上求一点 P,使得:(1)P 到 A(4,1)和 B(0,4)的距离之差最大;(2)P 到 A(4,1)和 C(3,4)的距离之和最小.【解析】(1)如图,B 关于 l 的对称点 B′(3,3).AB′:2x + y – 9 = 0由 解得 P(2,5).(2)C 关于 l 对称点由图象可知:|PA| + |PC|≥|AC′|当 P 是 AC′与 l 的交点时“=”成立,∴.例 3 如图,一束光线经过 P (2,1)射到直线 l:x + y + 1 = 0,反射后穿过点 Q (0,2)求:(1)入射光线所在直线 的方程; (2)沿这条光线从 P 到 Q 的长度.【解析】(1)设点 Q′(a,b)是 Q 关于直线 l 的对称点因为 QQ′⊥l,k1 = –1,所以又因为 Q′Q 的中点在直线 l 上,所以所以得,所以 Q′(–3,–1)因为 Q′在入射光线所在直线 l1上,设其斜率为 k,所以l1:即 2x – 5y + 1 = 0(2)设 PQ′与 l 的交点 M,由(1)知|QM| = |Q′M|所以|PM| + |MQ| = |PM| + |MQ′| = |PQ′| = 所以沿这光线从 P 到 Q 的长度为.入射光所在直线方程为 2x – 5y + 1 = 0.