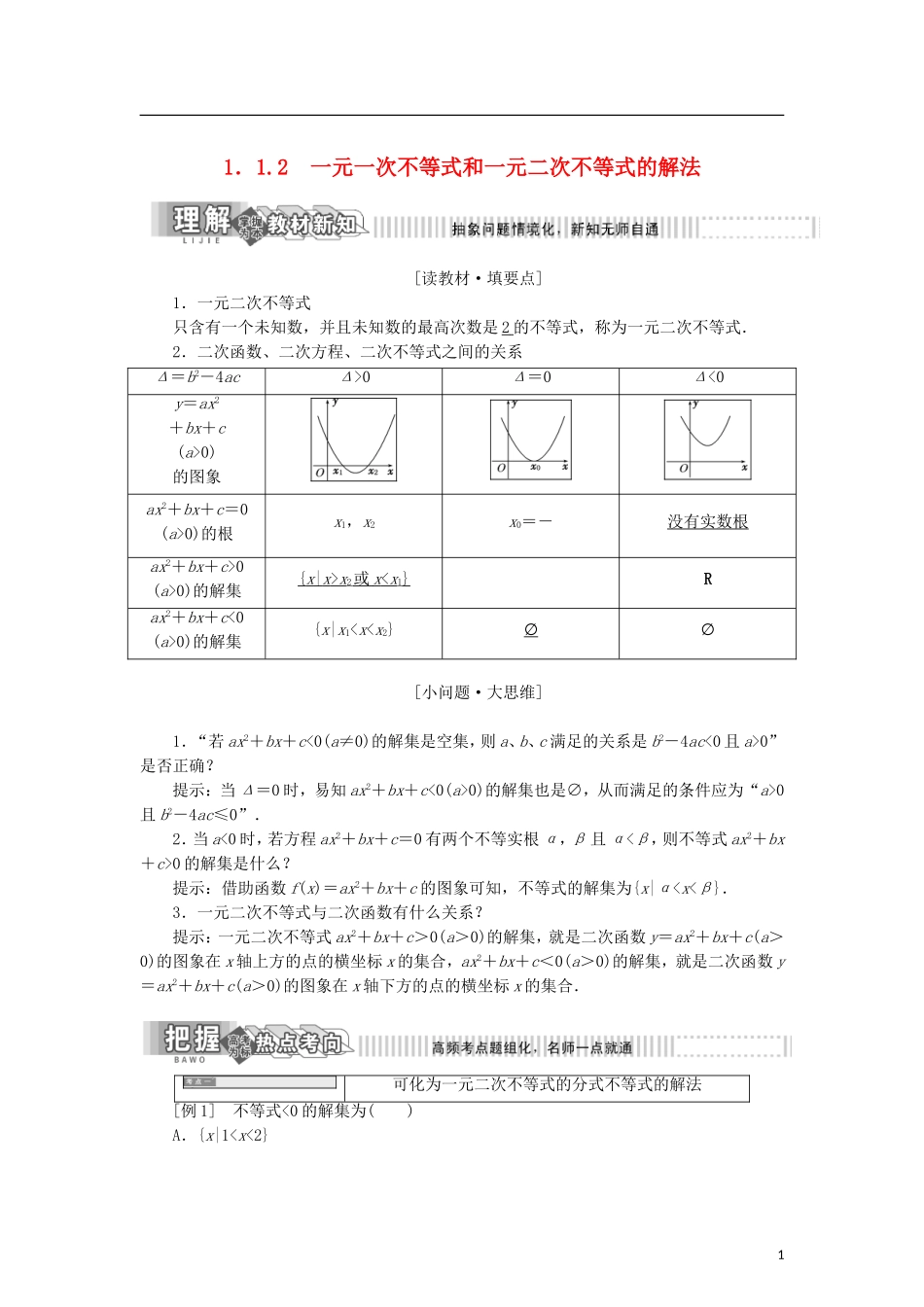
1.1.2 一元一次不等式和一元二次不等式的解法[读教材·填要点]1.一元二次不等式只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式.2.二次函数、二次方程、二次不等式之间的关系Δ=b2-4acΔ>0Δ=0Δ<0y=ax2+bx+c(a>0)的图象ax2+bx+c=0(a>0)的根x1,x2x0=-没有实数根ax2+bx+c>0(a>0)的解集{ x | x > x 2 或 x < x 1}Rax2+bx+c<0(a>0)的解集{x|x1
0”是否正确?提示:当 Δ=0 时,易知 ax2+bx+c<0(a>0)的解集也是∅,从而满足的条件应为“a>0且 b2-4ac≤0”.2.当 a<0 时,若方程 ax2+bx+c=0 有两个不等实根 α,β 且 α<β,则不等式 ax2+bx+c>0 的解集是什么?提示:借助函数 f(x)=ax2+bx+c 的图象可知,不等式的解集为{x|α0,a<0 讨论.[精解详析] 若 a=0,原不等式可化为-x+1<0,即 x>1.若 a<0,原不等式可化为(x-1)>0,即 x<或 x>1.若 a>0,原不等式可化为(x-1)<0(*)其解的情况应由与 1 的大小关系决定,故(1)当 a=1 时,由(*)式可得 x∈∅;(2)当 a>1 时,由(*)式可得