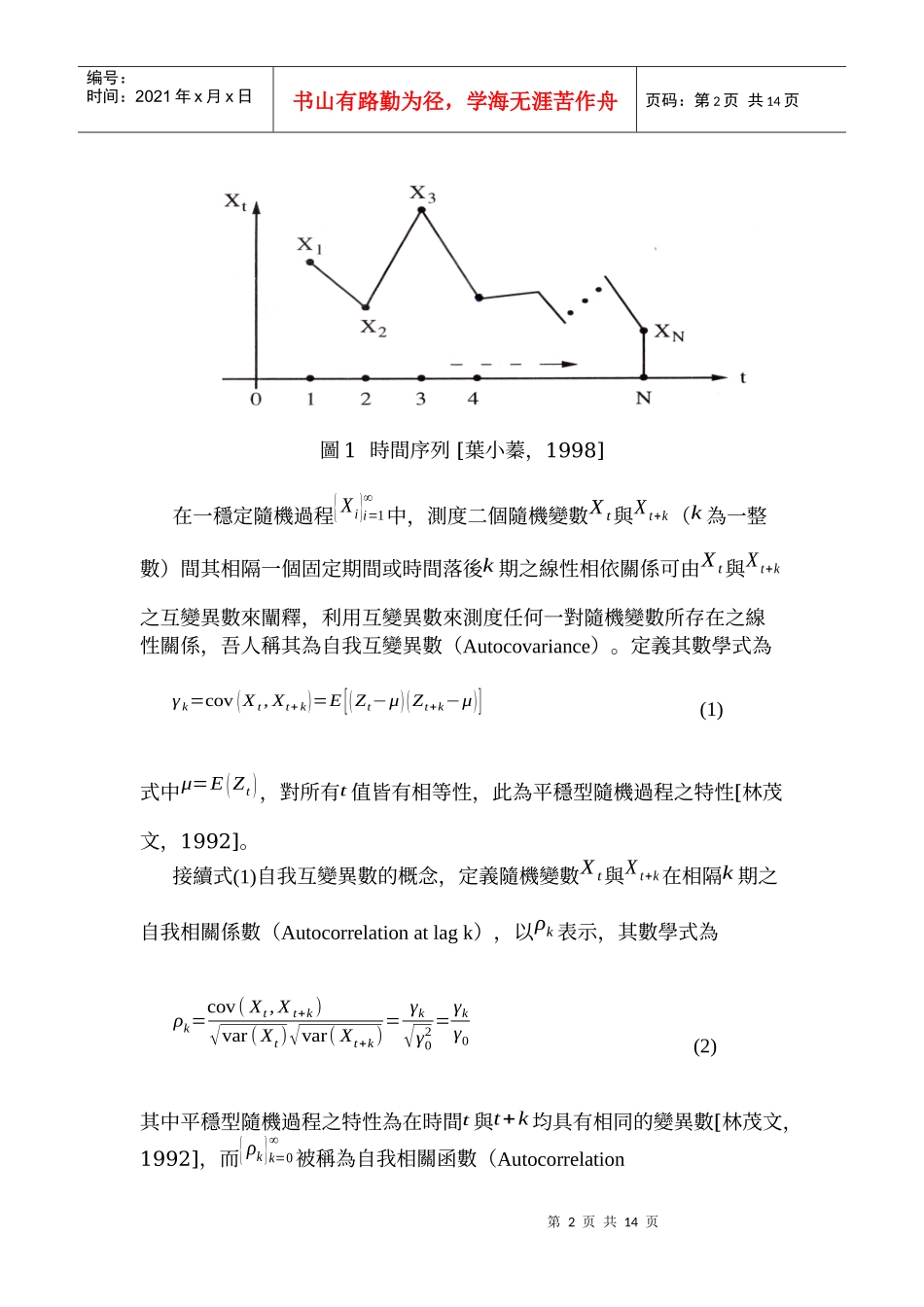
第1页共14页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共14页以時間序列分析法偵測台灣一等二級水準網之殘留系統誤差DetectingRemainedSystematicErrorsInTheFirst-OrderClassⅡLevelingNetworkofTaiwanByUsingTimeseries指導教授:許榮欣學生:李明一前言時間序列(Timeseries),係指以時間順序型態出現之一連串觀測值集合,或更確切的說,對某動態系統(DynamicSystem)隨時間連續觀察所產生有順序的觀測值集合。時間序列分析是一種數理統計的方法,它可以計算兩筆相近資料間的統計相關性,因此可用來判斷是否含有系統誤差。綜合上述,假如把時間序列分析的概念帶入水準測量中,吾人可加以利用的數據包含有測段閉合差、測段長、坡度、往返施測時…的氣溫及測段方位角等眾多數據[Vanicek,P.&Craymer,M.,1983]。時間序列分析法一組觀測值{X1,X2,...,XN},若沿著時間先後有順序地產生,則稱此組觀測值為一時間序列,而正整數N被稱為時間序列的長度[葉小蓁,1998]。任一時間序列均可延著時間軸作其對應的時間序列圖,如圖1。第2页共14页第1页共14页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共14页圖1時間序列[葉小蓁,1998]在一穩定隨機過程{Xi}i=1∞中,測度二個隨機變數Xt與Xt+k(k為一整數)間其相隔一個固定期間或時間落後k期之線性相依關係可由Xt與Xt+k之互變異數來闡釋,利用互變異數來測度任何一對隨機變數所存在之線性關係,吾人稱其為自我互變異數(Autocovariance)。定義其數學式為γk=cov(Xt,Xt+k)=E[(Zt−μ)(Zt+k−μ)](1)式中μ=E(Zt),對所有t值皆有相等性,此為平穩型隨機過程之特性[林茂文,1992]。接續式(1)自我互變異數的概念,定義隨機變數Xt與Xt+k在相隔k期之自我相關係數(Autocorrelationatlagk),以ρk表示,其數學式為ρk=cov(Xt,Xt+k)√var(Xt)√var(Xt+k)=γk√γ02=γkγ0(2)其中平穩型隨機過程之特性為在時間t與t+k均具有相同的變異數[林茂文,1992],而{ρk}k=0∞被稱為自我相關函數(Autocorrelation第3页共14页第2页共14页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共14页Function,ACF)。自我相關函數有如下之特性:[葉小蓁,1998](1)ρ0=1(2)−1≤ρj≤1,∀j∈{1,2,...}(3)ρj無單位(4)ρj=−ρj,∀j∈{1,2,...}平穩型時間序列(StationaryTimeSeries)係指一個時間序列其統計特性將不隨時間之變化而改變者,換言之,一個平穩型時間序列為一隨機過程之特殊實現值,且這種隨機過程之統計特性並不隨時間之變化而改變,即隨機過程{Xi}i=1∞需滿足以下三個條件:(1)E(Xi)=μ(2)var(Xi)=γ0(3)cov(Xi,Xi+m)=γm其中E表示期望值,var表示變異數,cov表示共變數,μ、γ0及γm均為有限的固定參數[Hsu,R,2002]。依上述平穩型時間序列特性,則每個觀測值可以表示為諸個互相獨立且具有相同機率分配之隨機變數序列at,at−1,at−2...之線性組合,而這些隨機變數通常假設為常態分佈,其期望值為0,變異數為σa2。因此,此種序列隨機變數at,at−1,at−2,...稱為白色干擾過程(WhiteNoiseProcess)。{at}之線性組合可以表示為Xt=μ+Ψ0at+Ψ1at−1+Ψ2at−2+...(3)式中μ與Ψj(j=0,1,2,...)為固定的參數值,Ψj稱為權數(Weight),通常第4页共14页第3页共14页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第4页共14页設Ψ0=1,μ為決定過程之平均水準。若一個時間序列為平穩型,即此序列為對固定均值上下隨機波動,若時間序列為非平穩型,則可知該序列無固定平均值。一般而言,假若權數{Ψj}為有限(Finite)或無限且收斂(InfiniteandConvergent)者,則可知此時間序列{Xt}為對平均數之平穩型時間序列,假若{Ψj}為無限且發散者(InfiniteandDivergent),則此數列為非平穩型時間序列[林茂文,1992]。將(3)式之係數Ψj以−θj替換,並僅討論前q個非零之權數,即當j>q時,Ψj=0。則Xt=μ+at−θ1at−1−θ2at−2−...−θqat−q(4)式中(1,−θ1,−θ2,...,−θq)亦稱為震動影響或記憶函數(Shock-EffectorMemoryFunction),表示震動at將持續影響t,t+1,.....