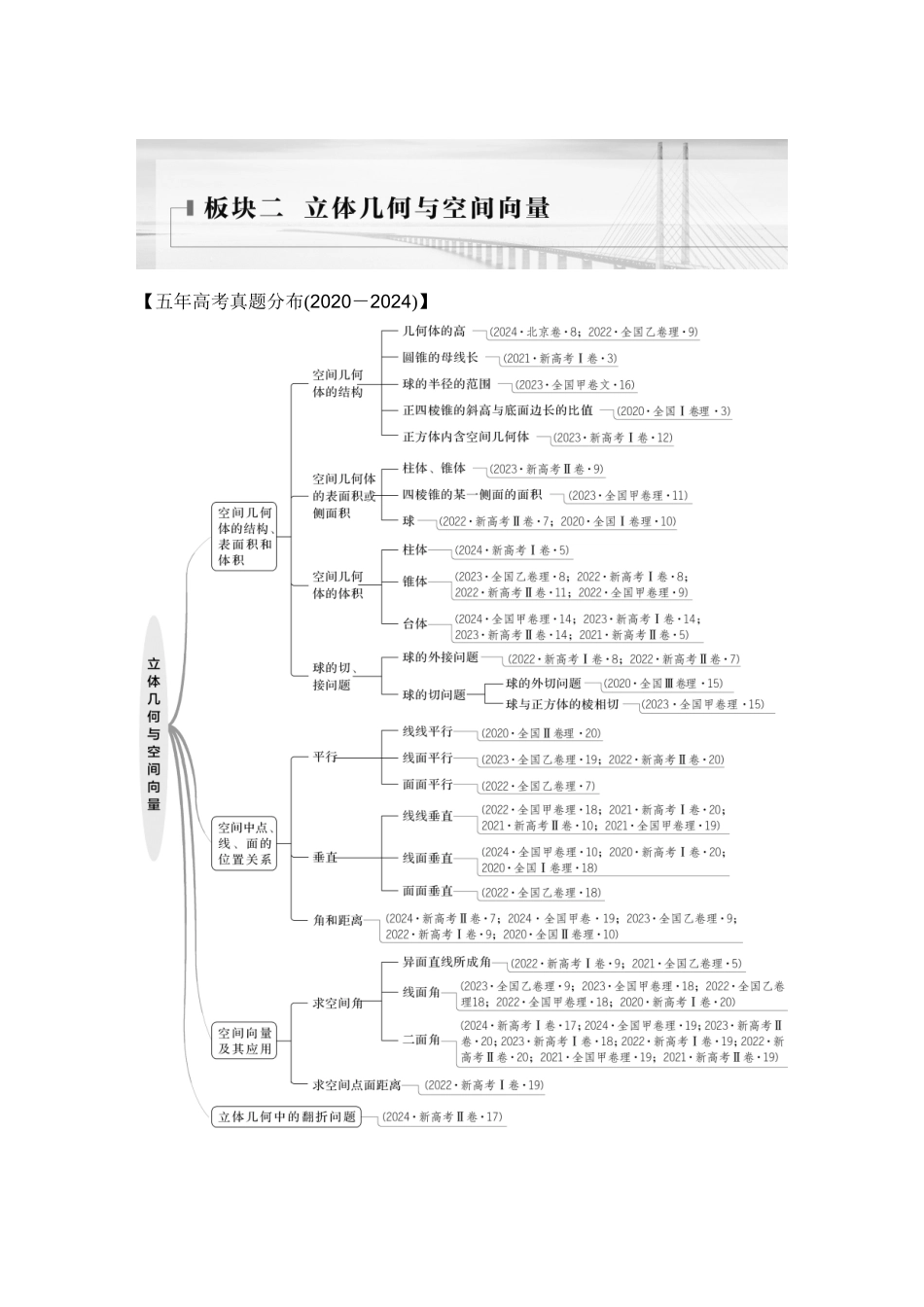
【五年高考真题分布(2020-2024)】微专题 8 空间几何体的表面积和体积高考定位 空间几何体的表面积和体积是高考考查的重点内容,常以选择题、填空题为主,要求考生要有较强的空间想象能力和计算能力,难度为中低档.【真题体验】1.(2024·新高考Ⅰ卷)已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为,则圆锥的体积为( )A.2πB.3πC.6πD.9π答案 B解析 设圆柱和圆锥的底面半径均为 r,因为它们的高均为,且侧面积相等,所以 2πr×=πr,得 r2=9,所以圆锥的体积 V=πr2×=3π,故选 B.2.(2023·全国甲卷)在三棱锥 P-ABC 中,△ABC 是边长为 2 的等边三角形,PA=PB=2,PC=,则该棱锥的体积为( )A.1B.C.2D.3答案 A解析 如图,取 AB 的中点 D,连接 PD,CD,因为△ABC 是边长为 2 的等边三角形,PA=PB=2,所以 PD⊥AB,CD⊥AB,所以 PD=CD=,又 PC=,所以 PD2+CD2=PC2,所以 PD⊥CD,又 AB∩CD=D,AB,CD⊂平面 ABC,所以 PD⊥平面 ABC,所以 VP-ABC=·S△ABC·PD=××2××=1,故选 A.3.(2024·天津卷)一个五面体 ABC-DEF.已知 AD∥BE∥CF,且两两之间距离为1,AD=1,BE=2,CF=3,则该五面体的体积为( )A.B.+C.D.-答案 C解析 因为 AD,BE,CF 两两平行,且两两之间距离为 1,则该五面体可以看作底面边长为 1 的正三棱柱的一部分,然后分成一个侧棱长为 1 的三棱柱和一个底面为梯形的四棱锥,如图,其中三棱柱的体积等于棱长均为 1 的直三棱柱的体积,四棱锥的高为,底面是上底为 1、下底为 2、高为 1 的梯形,故该五面体的体积V=×1××1+××=,故选 C.4.(2024·全国甲卷)已知圆台甲、乙的上底面半径均为 r1,下底面半径均为 r2,圆台的母线长分别为 2(r2-r1),3(r2-r1),则圆台甲与乙的体积之比为________.答案 解析 两圆台的上、下底面积对应相等,则两圆台的体积之比为高之比,根据母线与半径的关系可得甲与乙的体积之比为==.【热点突破】热点一 空间几何体的侧面积、表面积例 1 (1)(2024·新乡二模)设圆台的上、下底面的半径之比为 1∶2,侧面积为18π,且上底面半径为质数,则该圆台的母线长为( )A.2B.3C.5D.6(2)(2024·河南部分学校模拟)如图 1 所示,宫灯又称宫廷花灯,是中国彩灯中富有特色的汉民族传统手工艺品之一.图 2 是小明为自家设计的一个花灯的直观图,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱...