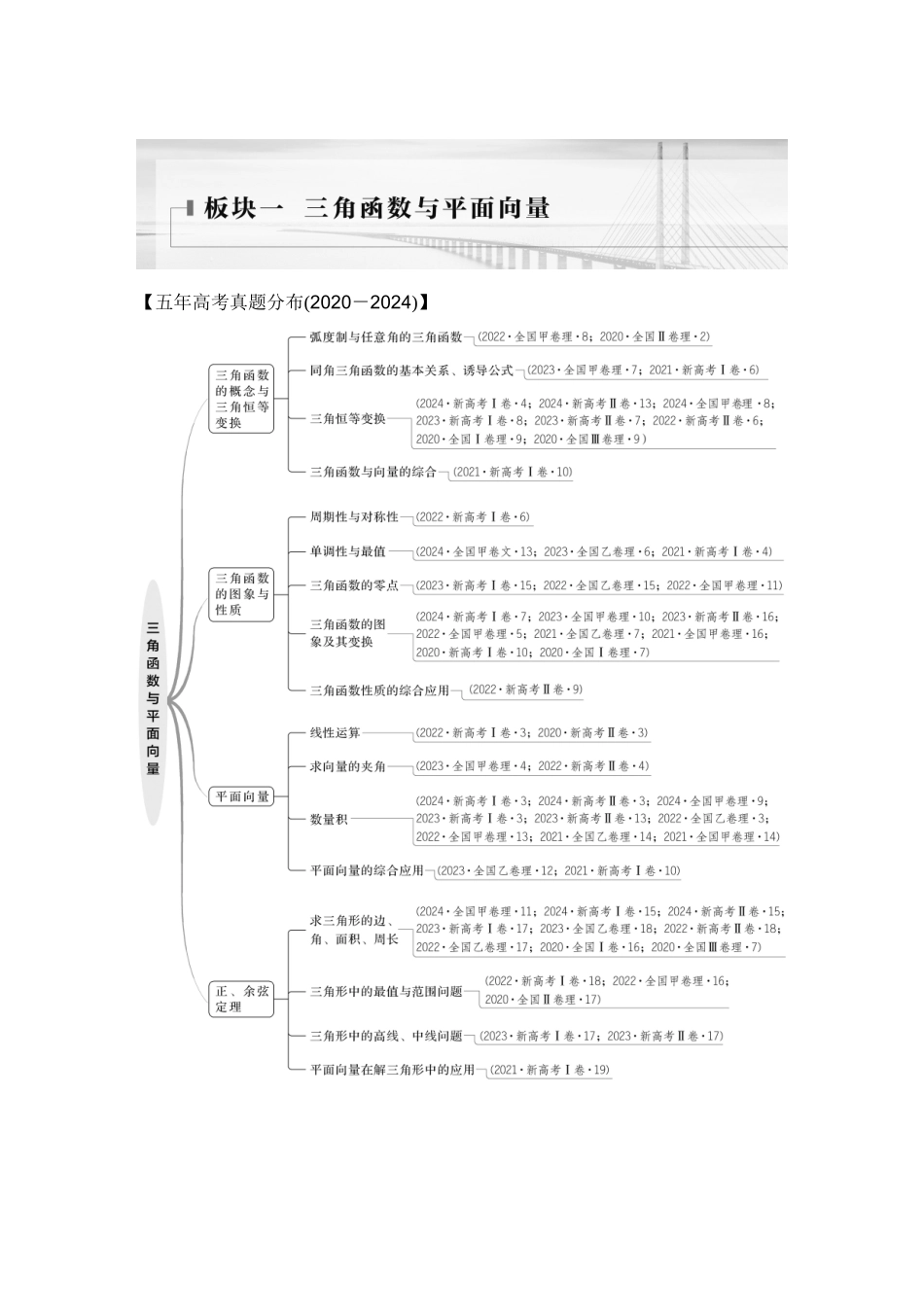
【五年高考真题分布(2020-2024)】微专题 1 三角恒等变换高考定位 1.三角函数的化简与求值是高考的命题热点,其中同角三角函数的基本关系、诱导公式是解决计算问题的工具; 2.三角恒等变换是利用三角恒等式(两角和与差、二倍角的正弦、余弦、正切公式)进行变换,“角”的变换是三角恒等变换的核心; 3.以选择、填空题的形式出现或隐含于解答题中,难度一般为中档偏下.【真题体验】1.(2021·全国乙卷)cos2-cos2=( )A.B.C.D.答案 D解析 因为 cos=sin=sin ,所以 cos2-cos2=cos2-sin2=cos=cos =.故选 D.2.(2023·新高考Ⅱ卷)已知 α 为锐角,cos α=,则 sin =( )A.B.C.D.答案 D解析 由题意,cos α==1-2sin2,得 sin2===,又 α 为锐角,所以 sin>0,所以 sin=,故选 D.3.(2024·全国甲卷)已知=,则 tan=( )A.2+1B.2-1C.D.1-答案 B解析 根据题意有=,即 1-tan α=,所以 tan α=1-,所以 tan===2-1.4.(2024·新高考Ⅱ卷)已知 α 为第一象限角,β 为第三象限角,tan α+tan β=4,tan αtan β=+1,则 sin(α+β)=________.答案 -解析 由题知 tan(α+β)===-2,即 sin(α+β)=-2cos(α+β),又 sin2(α+β)+cos2(α+β)=1,可得 sin(α+β)=±.由 2kπ<α<2kπ+,k∈Z,2mπ+π<β<2mπ+,m∈Z,得 2(k+m)π+π<α+β<2(k+m)π+2π,k+m∈Z.又 tan(α+β)<0,所以 α+β 是第四象限角,故 sin(α+β)=-.【热点突破】热点一 化简问题例 1 (1)(2024·宜昌联考)=( )A.B.C.D.2(2)(2024·西安模拟)等于( )A.B.C.D.1答案 (1)C (2)C解析 (1)===.(2)====cos 30°=.规律方法 求解三角函数的化简问题常用以下原则:一看角:通过看角之间的差别与联系,可把角进行合理转化;二看函数名称:如果函数名称不同,那么可利用公式将函数名称进行转化,常见的有“切化弦”;三看结构特征:通过看结构特征,找到变形的方向,常见的有“遇到分式要通分”“遇到根式要升幂”等.训练 1 化简:(1)=________;(2)(tan 10°-)·=________.答案 (1)4sin α (2)-2解析 (1)===4sin α.(2)原式=·==-2.热点二 求值问题例 2 (1)(2024·衡阳模拟)已知 cos=,则 sin 等于( )A.-B.C.-D.(2)(2024·河南部分学校联考)若锐角 α,β 满足 sin(α-β)=,cos=,则 cos=________.答案 (1)D (2)...