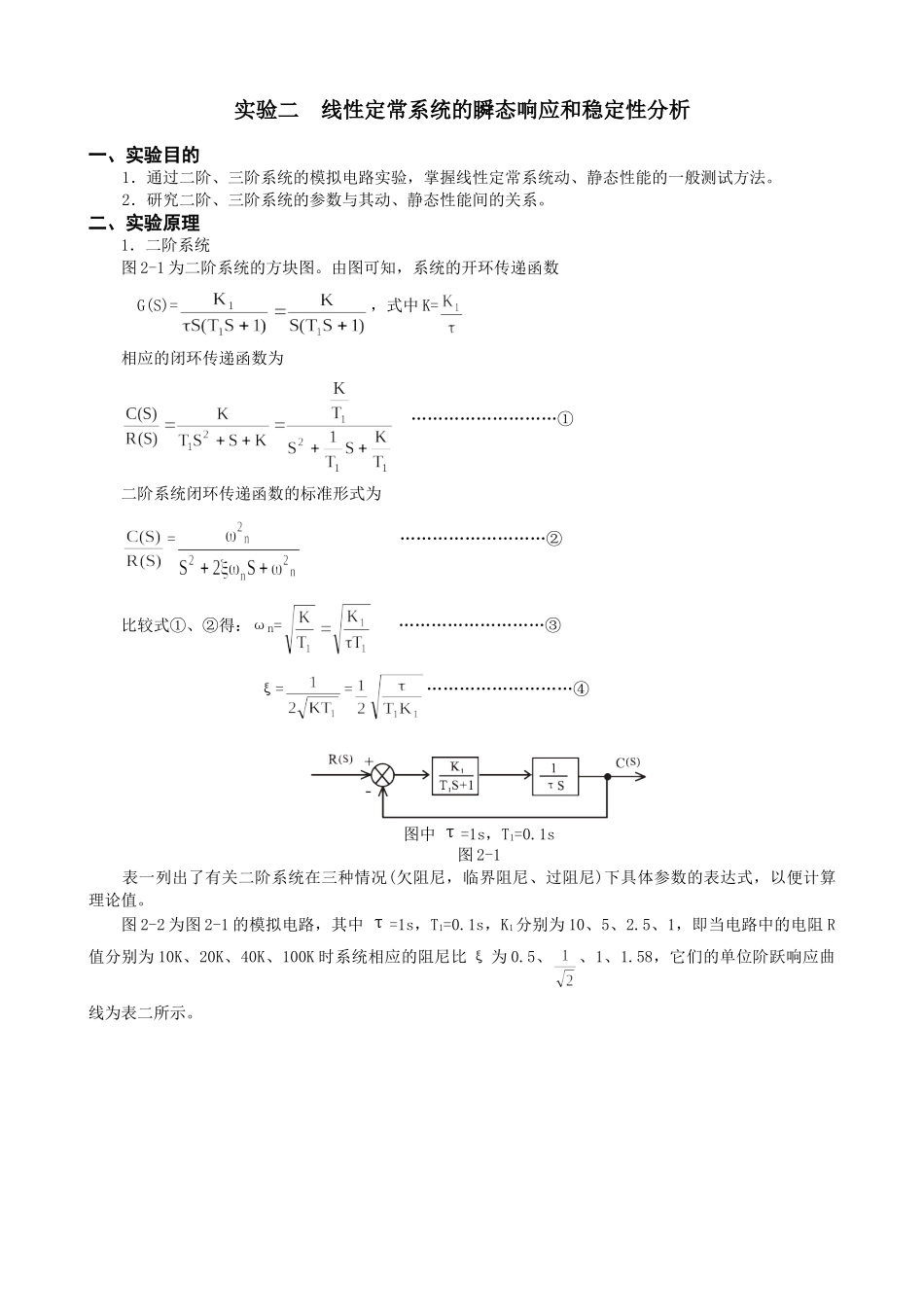
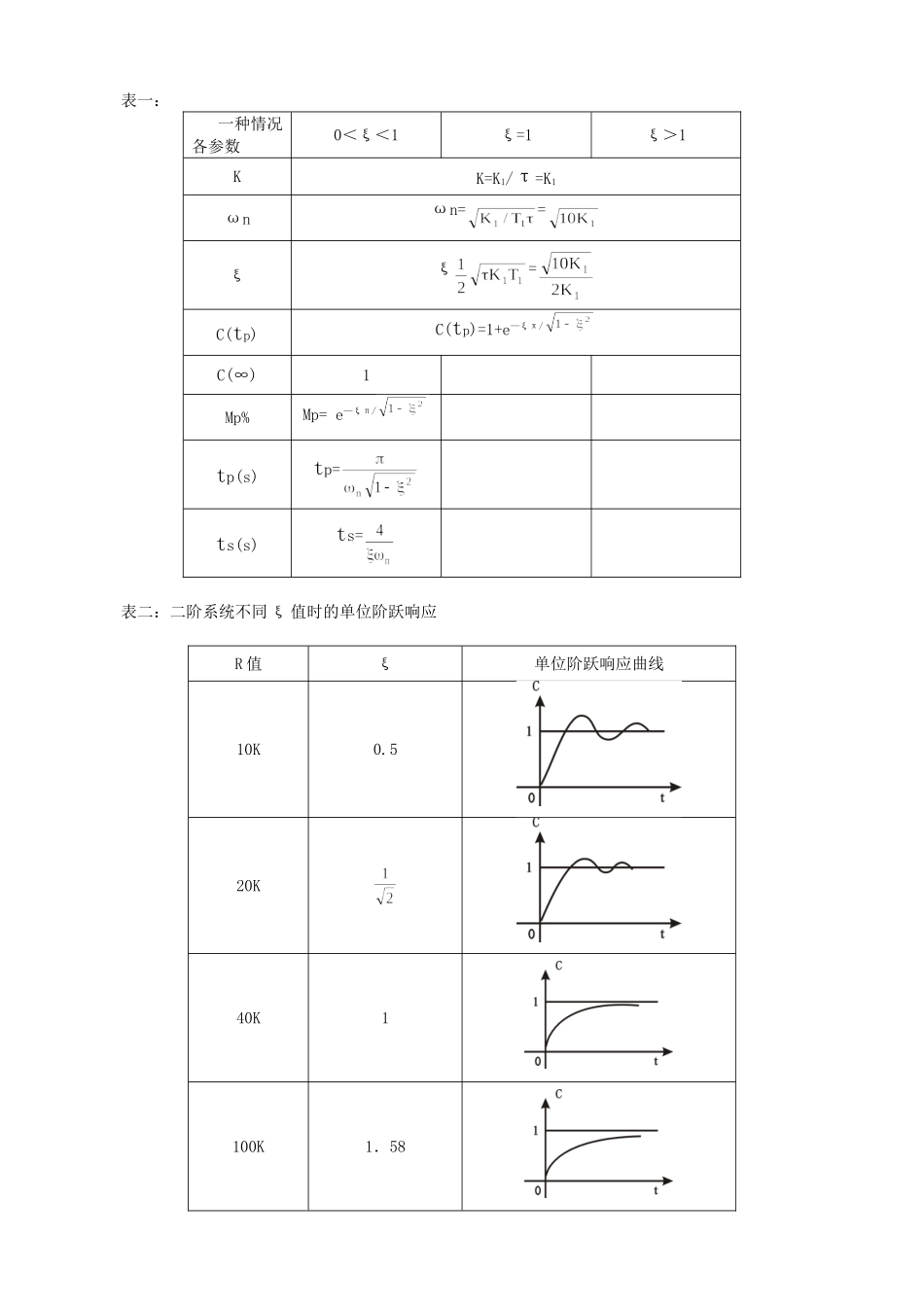
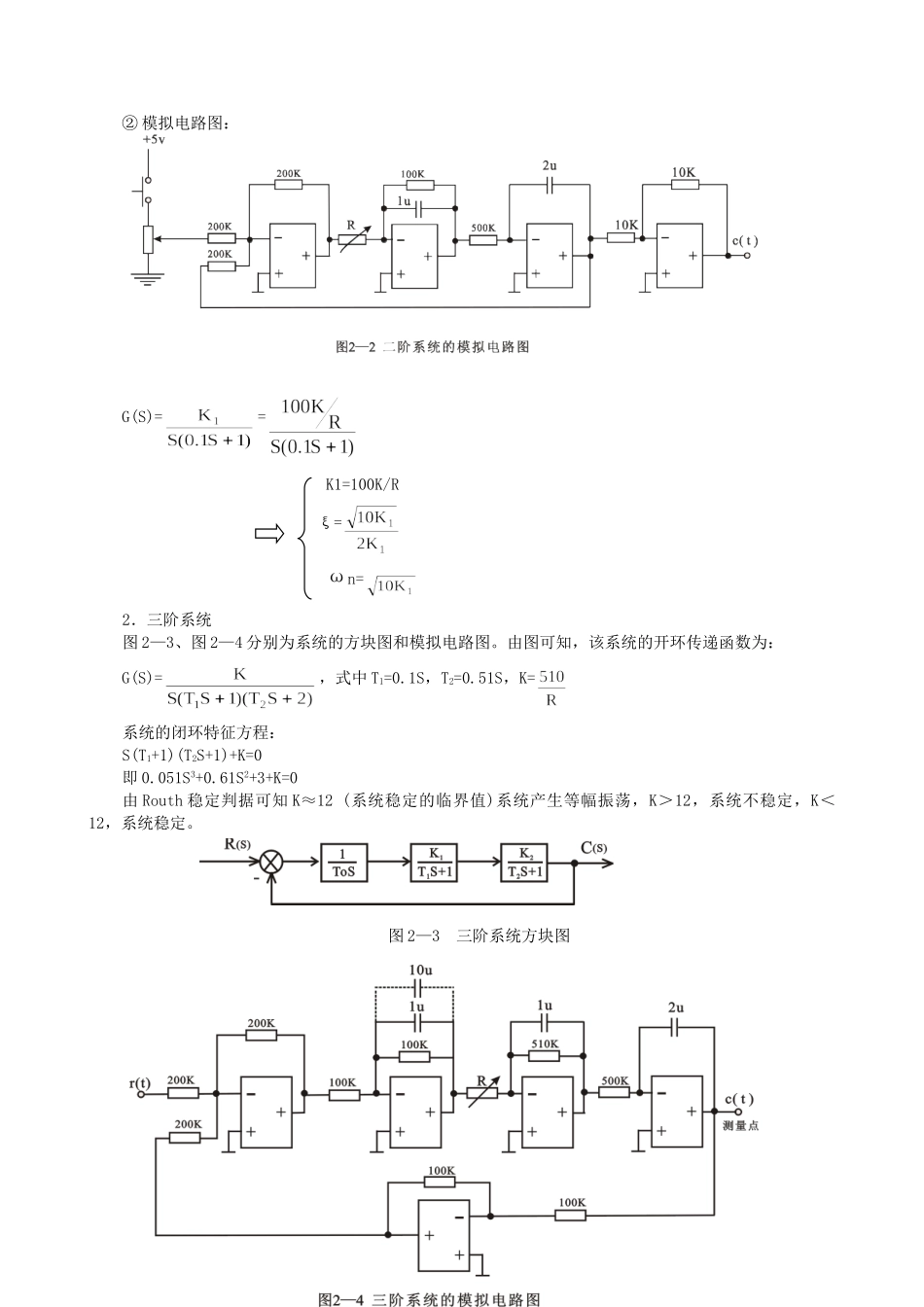
实验二 线性定常系统的瞬态响应和稳定性分析一、实验目的1.通过二阶、三阶系统的模拟电路实验,掌握线性定常系统动、静态性能的一般测试方法。2.研究二阶、三阶系统的参数与其动、静态性能间的关系。二、实验原理1.二阶系统图 2-1 为二阶系统的方块图。由图可知,系统的开环传递函数G(S)=,式中 K=相应的闭环传递函数为 ………………………①二阶系统闭环传递函数的标准形式为= ………………………②比较式①、②得:ωn= ………………………③ ξ==………………………④图中 τ=1s,T1=0.1s图 2-1表一列出了有关二阶系统在三种情况(欠阻尼,临界阻尼、过阻尼)下具体参数的表达式,以便计算理论值。图 2-2 为图 2-1 的模拟电路,其中 τ=1s,T1=0.1s,K1分别为 10、5、2.5、1,即当电路中的电阻 R值分别为 10K、20K、40K、100K 时系统相应的阻尼比 ξ 为 0.5、、1、1.58,它们的单位阶跃响应曲线为表二所示。表一:一种情况各参数0<ξ<1ξ=1ξ>1KK=K1/τ=K1ωnωn==ξξ=C(tp)C(tp)=1+e—ξπ/C(∞)1Mp%Mp= e—ξπ/tp(s)tp=ts(s)ts=表二:二阶系统不同 ξ 值时的单位阶跃响应R 值ξ单位阶跃响应曲线10K0.520K40K1100K1.58② 模拟电路图: G(S)== K1=100K/R ξ= ωn=2.三阶系统图 2—3、图 2—4 分别为系统的方块图和模拟电路图。由图可知,该系统的开环传递函数为:G(S)=,式中 T1=0.1S,T2=0.51S,K=系统的闭环特征方程:S(T1+1)(T2S+1)+K=0即 0.051S3+0.61S2+3+K=0 由 Routh 稳定判据可知 K≈12 (系统稳定的临界值)系统产生等幅振荡,K>12,系统不稳定,K<12,系统稳定。 图 2—3 三阶系统方块图图 2—3 三阶系统方块图三、实验内容1.通过对二阶系统开环增益的调节,使系统分别呈现为欠阻尼 0<ξ<1(R=10K,K=10),临界阻尼ξ=1(R=40K,K=2.5)和过阻尼 ξ>1(R=100K,K=1)三种状态,并用示波器记录它们的阶跃响应曲线。2.通过对二阶系统开环增益 K 的调节,使系统的阻尼比 ξ==0.707(R=20K,K=5),观测此时系统在阶跃信号作用下的动态性能指标:超调量 Mp,上升时间 tp 和调整时间 ts。3.研究三阶系统的开环增益 K 或一个慢性环节时间常数 T 的变化对系统动态性能的影响。4.由实验确定三阶系统稳定的临界 K 值,并与理论计算结果进行比较。四、实验步骤准备工作:将“信号发生器单元”U1 的 ST 端和+5V 端用“短路块”短接,并使运放反馈网络上的场效应管 3DJ...