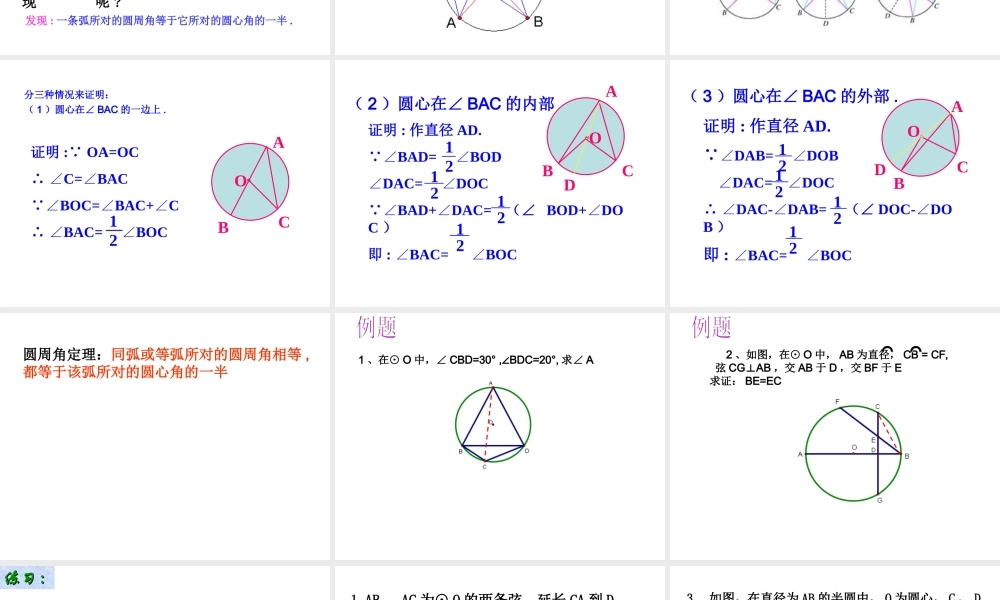
§ 24.1.4 圆周角(第 1 课时)重点:圆周角的概念,圆周角定理难点:圆周角定理的分情况证明知识点 : (1) 圆周角定义 (2) 圆心角和圆周角的区别与联系 (3) 圆周角定理及其证明 复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角圆心角。考考你:你能仿照圆心角的定义, 给下图中象∠ ACB 这样的角下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角圆周角. 探索:判断下列各图中,哪些是圆周角,为什么? 活动活动 22 问题 1 同弧(弧 AB )所对的圆心角∠ AOB 与圆周角∠ ACB 的大小关系是怎样的? 问题 2 同弧(弧 AB )所对的圆周角∠ ACB 与圆周角∠ ADB 的大小关系是怎样的? 画一个圆心角 , 然后再画同弧所对的圆周角 .1. 同一条弧你能画多少个圆周角 ? 多少个圆 心角 ? 用量角器量一量这些 圆周角你有何发现?2. 再用量角器量出圆心角的度数 , 你有何发现 呢 ?发现 : 一条弧所对的圆周角等于它所对的圆心角的一半 .ABO探索探索2:2:发现 : 在同圆 ( 或等圆 ) 中 , 同弧或等弧所对的圆周角相等探究探究怎样证明同弧或等弧所对的圆周角相等 , 都等于该弧所对的圆心角的一半? 做一做做一做 问题 1 在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?分三种情况来证明:( 1 )圆心在∠ BAC 的一边上 . AOBC12证明 : OA=OC ∴ ∠C=BAC∠ ∠BOC=BAC+C∠∠ ∴ ∠BAC= BOC∠( 2 )圆心在∠ BAC 的内部 .OABCD1212证明 : 作直径 AD. ∠BAD= BOD∠∠DAC= DOC∠ ∠BAD+DAC= ∠(∠ BOD+DO∠C )即 : BAC= BOC∠∠1212OABC( 3 )圆心在∠ BAC 的外部 .D证明 : 作直径 AD. ∠DAB= DOB∠ ∠DAC= DOC∠ ∴ ∠DAC-DAB= ∠(∠ DOC-DO∠B )即 : BAC= BOC∠∠12121212圆周角定理:同弧或等弧所对的圆周角相等 ,都等于该弧所对的圆心角的一半 1 、在⊙ O 中,∠ CBD=30° , BDC=20°,∠求∠ A 2 、如图,在⊙ O 中, AB 为直径, CB = CF, 弦 CGAB⊥,交 AB 于 D ,交 BF 于 E 求证: BE=EC⌒⌒⌒⌒ 求圆中角 X 的度数BAO.70°xAO.X120°练习练习 ::1.AB 、 AC 为⊙ O 的两条弦,延长 CA 到 D ,使 AD=AB ,如果∠ ADB=35° ,求∠ BOC 的度数。⌒⌒2 、如图,在⊙ O 中, BC=2DE , ∠ BOC=84° ,求∠ A 的...