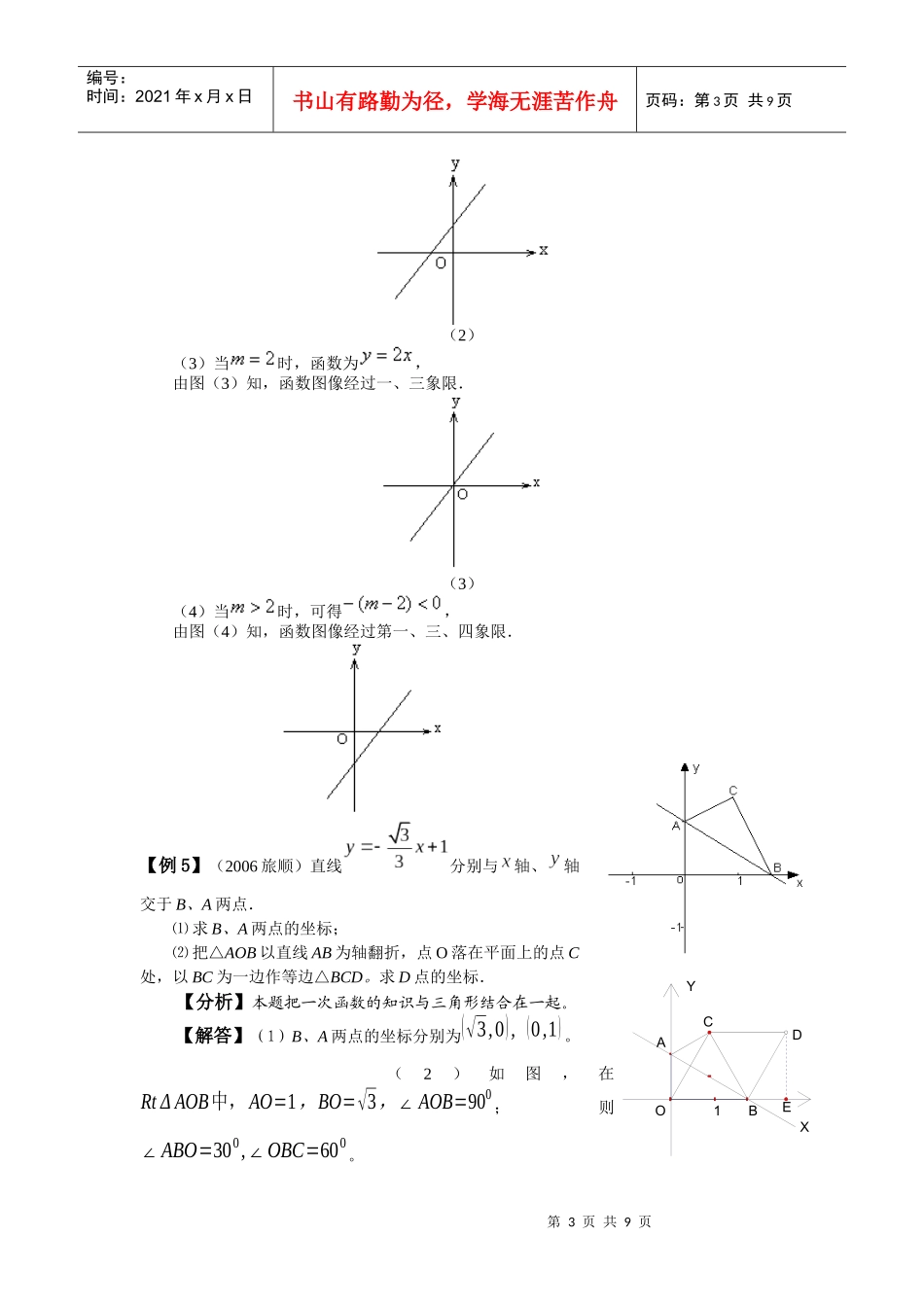
第1页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共9页§3.2一次函数复习目标1.一次函数:若两个变量x、y间的关系式可以表示成y=kx+b(k、b为常数,k≠0)的形式,则称y是x的一次函数;特别地,当b=0时,称y是x的正比例函数.2.一次函数的图象:一次函数y=kx+b的图象是经过点(0,b),(-,0)的一条直线,正比例函数y=kx的图象是经过原点(0,0)的一条直线,如下表所示.3.一次函数的性质:y=kx+b(k、b为常数,k≠0)当k>0时,y的值随x的值增大而增大;当k<0时,y的值随x值的增大而减小.4.直线y=kx+b(k、b为常数,k≠0)时在坐标平面内的位置与k在的关系.⑴直线经过第一、二、三象限(直线不经过第四象限);⑵直线经过第一、三、四象限(直线不经过第二象限);⑶直线经过第一、二、四象限(直线不经过第三象限);⑷直线经过第二、三、四象限(直线不经过第一象限)。5.一次函数表达式的求法:确定一次函数表达式常用待定系数法,其中确定正比例函数表达式,只需一对x与y的值,确定一次函数表达式,需要两对x与y的值。典例精析【例1】若函数是一次函数,求的值,并写出解析式。【分析】本题需注意两个方面,①x的次数为1②x的系数不等于零。【解答】由题意得,,则,因为,所以则所以它的解析式为y=−2x+3【例2】(2006遂宁)地表以下岩层的温度t(0C)随时着所处的深度h(千米)的变化而变化,t与h在一定范围内近似成一次函数关系(1)根据下表,求t(0C)与h(千米)之间的函数关系式;213mymxm12m1m01m1m1m第2页共9页第1页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共9页(2)求当岩层温度达到7700C时,岩层所处的深度为多少千米?温t(0C)···90110300···深度h(千米)···248···【分析】本题用待定系数法确定一次函数的关系式。【解答】⑴设t=kh+b,选取两组值代入可得方程组:{2k+b=90¿¿¿¿解得{k=10¿¿¿¿,所以所求的函数关系式t=10h+70⑵当t=770时,h=70。所以当岩层温度达到7700C时,岩层所处的深度为70千米。【例3】已知一次函数y=kx+b的图象如图所示,当x<0时,y的取值范围是()A.y>0B、y<0C、-2<y<0D.y<-2【分析】由图象可知一次函数y=kx+b过一、三、四象限,当x<0时,y对应的值在-2的下方.故选D【解答】D【例4】已知一次函数,试讨论其图像经过哪些象限?【分析】由的正负性,分情况画出草图,进而判断直线所经过的象限.【解答】(1)当时,可得,由图(1)知函数图像经过第一、二、四象限.(1)(2)当时,可得,由图(2)知,函数图像经过第一、二、三象限.)2(mmxy2,mm第3页共9页第2页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共9页(2)(3)当时,函数为,由图(3)知,函数图像经过一、三象限.(3)(4)当时,可得,由图(4)知,函数图像经过第一、三、四象限.【例5】(2006旅顺)直线分别与轴、轴交于B、A两点.⑴求B、A两点的坐标;⑵把△AOB以直线AB为轴翻折,点O落在平面上的点C处,以BC为一边作等边△BCD。求D点的坐标.【分析】本题把一次函数的知识与三角形结合在一起。【解答】(1)B、A两点的坐标分别为(√3,0),(0,1)。(2)如图,在RtΔAOB中,AO=1,BO=√3,∠AOB=900;则∠ABO=300,∠OBC=600。YXEDCBAO1第4页共9页第3页共9页62Ox(h)y(m)3060乙甲50图象与信息编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第4页共9页①若以BC为一边向左下方作等边△BCD,则D点刚好与原点O重合,此时D点的坐标为(0,0)。②若以BC为一边向右上方作等边△BCD,过D点作DE⊥x轴于点E。由已知可得在RtΔDBE中,∠DBE=600,BD=√3,∠DEB=900∴BE=√32,DE=32则此时D点的坐标为(3√32,32).课内巩固l.下列关于x的函数中,是一次函数的是()2.如果直线y=kx+b经过一、二、四象限,那么有()A.k>0,b>0B.k>0,b<0C.k<0,b<0D.k<0,b>03.油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量Q(升)与流出时间t(分钟)的函数关系是()A.Q=0.2tB.Q=2...