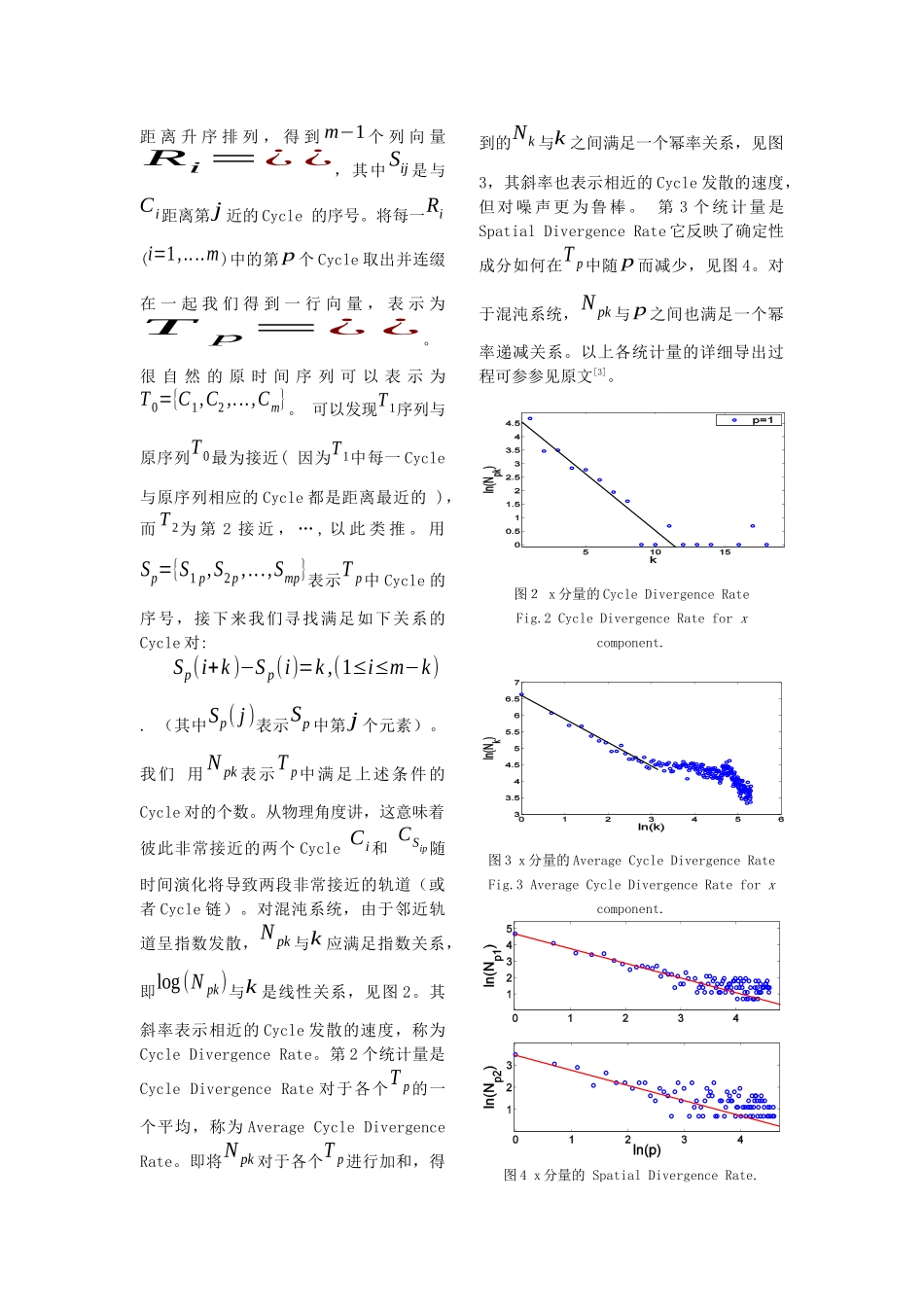
单涡卷蔡氏电路的非线性时间序列分析张捷孙俊峰MichaelSmall香港理工大学电子及资讯工程学系,香港九龙摘要:蔡氏电路表现出单涡卷引子时,其输出为包含一明显周期成分的伪周期时间序列。对于这种时间序列我们采用几种最新提出的方法来分析和刻画其混沌动力学特性,包括将时间序列划分为单个Cycle,并在时域和相空间中研究其相关性质,以及对系统重现时间分布进行统计。这些新的方法进一步加深了我们对蔡氏电路单涡卷混沌吸引子的认识。关键词:单涡卷蔡氏电路;伪周期时间序列;复杂网络;重现时间;混沌近年来,非线性科学及混沌理论在保密通信,功率电子学,自动控制,生物医学以及许多其他工程领域获得了广泛的应用[1],比如利用混沌同步实现保密通信,和通过反馈方法对混沌奇怪吸引子的不稳定周期轨道进行控制,已成为通讯领域[2]和自控领域的研究热点,并已进入到应用阶段。在电路与系统研究中蔡氏电路一直是一个热点.它是目前众多混沌电路中最具代表性的一种,其典型的电路结构已成为理论和实验研究混沌的一个范例。蔡氏电路能够展现出一系列复杂的混沌动力学特性,但对于其单涡卷吸引子的情形研究还较少。蔡氏电路表现出单涡卷吸引子时,其x分量包含一明显的周期成分,见图1。所对应的时间序列为一伪周期时间序列。传统的基于混沌理论的非线性时间序列分析方法对于伪周期时间序列往往不适合,这是因为伪周期时间序列内在的周期性可能会掩盖原本存在的混沌特性[3]。此外噪声不可避免的会引起传统的混沌不变量如关联维数,李亚普诺夫指数的失效[3]。本文采用新的伪周期时间序列的分析方法[3,4]以及状态复现时间(RecurrenceTime)对蔡氏电路单涡卷吸引子x分量进行分析,目的是对这种时间序列的确定性成分(如混沌)进行多方面和更为鲁棒的刻画,从而对系统的混沌动力学特性有更深入的理解。这些刻画还可以用于系统辨识等其他目的。1时间序列的混沌特性检测1.1.Cycle的时域相关性图1(a)蔡氏电路的单涡卷混沌吸引子。(b)蔡氏电路的x分量。对应的方程为:{x'=−9.2(y−x−h(x))¿{y'=x−y−z¿¿¿¿,h(x)=m1x+(m0−m1)∗¿¿['|x−1|−|x+1|]/2(m0=−8/7,m1=−5/7)Fig.1(a)single-scroll.chaoticattractorfromChuacircuit(b)Correspondingtimeseries.我们首先将时间序列{xt}t=1N(N个观测值)按照局部极大(或极小)值分割为m个连续的Cycle(周期)。对每对CyclesCi和Cj(i,j=1,2,...,N,i≠j),我们用其相关系数来度量它们的相似性或者在相空间中的距离[3].事实上,两个Cycle如果具有高的相关系数,它们在相空间中的距离也是小的。对每一CycleCi,我们将其他所有m−1个Cycle按照其与Ci的距离升序排列,得到m−1个列向量Ri=¿¿,其中Sij是与Ci距离第j近的Cycle的序号。将每一Ri(i=1,....m)中的第p个Cycle取出并连缀在一起我们得到一行向量,表示为Tp=¿¿。很自然的原时间序列可以表示为T0={C1,C2,...,Cm}。可以发现T1序列与原序列T0最为接近(因为T1中每一Cycle与原序列相应的Cycle都是距离最近的),而T2为第2接近,…,以此类推。用Sp={S1p,S2p,...,Smp}表示Tp中Cycle的序号,接下来我们寻找满足如下关系的Cycle对:Sp(i+k)−Sp(i)=k,(1≤i≤m−k).(其中Sp(j)表示Sp中第j个元素)。我们用Npk表示Tp中满足上述条件的Cycle对的个数。从物理角度讲,这意味着彼此非常接近的两个CycleCi和CSip随时间演化将导致两段非常接近的轨道(或者Cycle链)。对混沌系统,由于邻近轨道呈指数发散,Npk与k应满足指数关系,即log(Npk)与k是线性关系,见图2。其斜率表示相近的Cycle发散的速度,称为CycleDivergenceRate。第2个统计量是CycleDivergenceRate对于各个Tp的一个平均,称为AverageCycleDivergenceRate。即将Npk对于各个Tp进行加和,得到的Nk与k之间满足一个幂率关系,见图3,其斜率也表示相近的Cycle发散的速度,但对噪声更为鲁棒。第3个统计量是SpatialDivergenceRate它反映了确定性成分如何在Tp中随p而减少,见图4。对于混沌系统,Npk与p之间也满足一个幂率递减关系。以上各统计量的详细导出过程可参参见原文[3]。图2x分量的CycleDivergenceRateFig.2CycleDivergenceRateforxcomponent.图3x分...