小学数学五大几何模型总结VIP免费

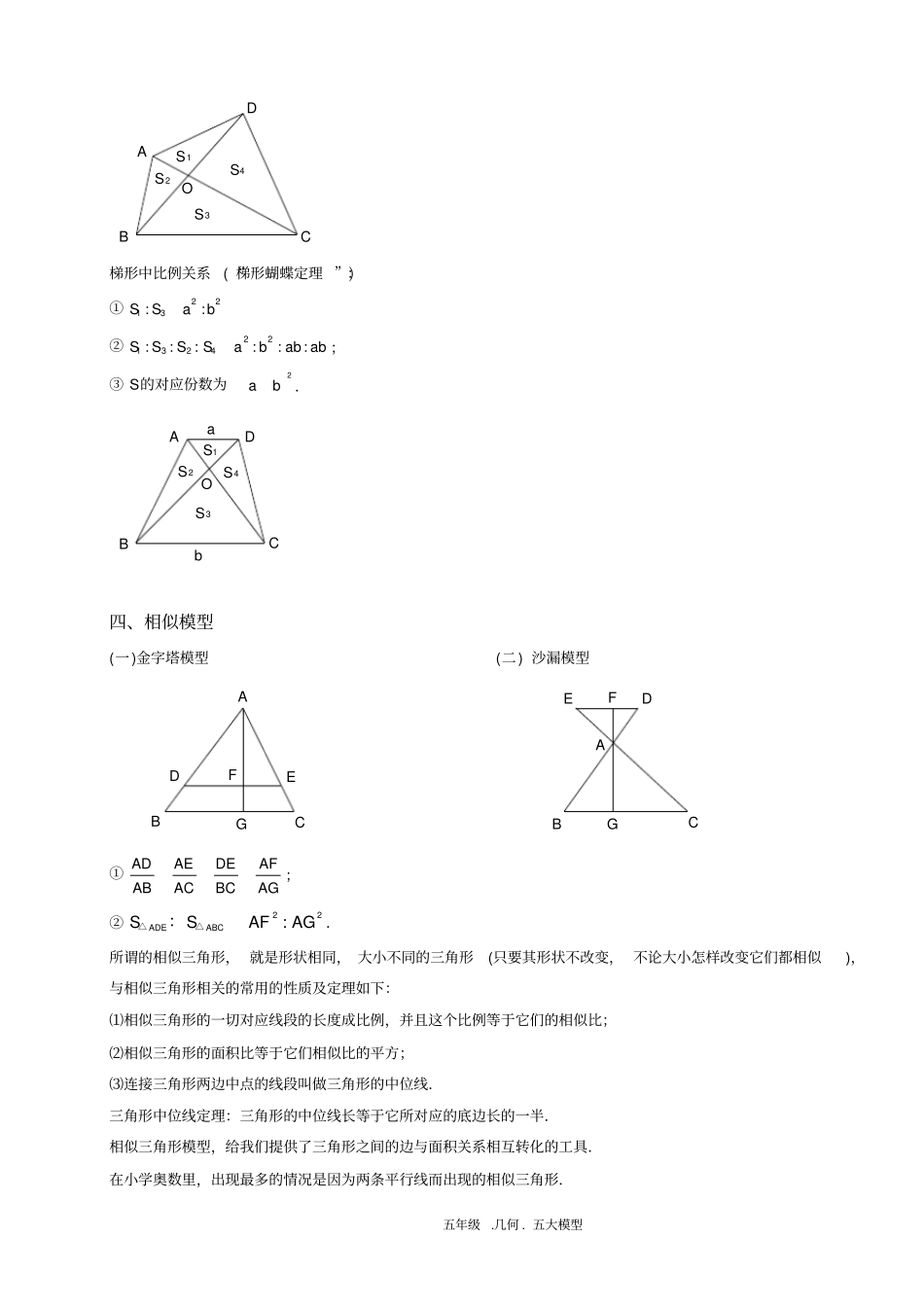
五年级.几何.五大模型五大模型（二）知识框架一、等积模型DCBA①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形，如右图ACDBCDSS△△；反之，如果ACDBCDSS△△，则可知直线AB平行于CD．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、共角定理（鸟头定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．:():()ABCADESSABACADAE△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)：①1243::SSSS或者1324SSSS②1243::AOOCSSSS蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．五年级.几何.五大模型S4S3S2S1ODCBA梯形中比例关系(“梯形蝴蝶定理”)：①2213::SSab②221324::::::SSSSababab；③S的对应份数为2ab．ABCDObaS3S2S1S4四、相似模型(一)金字塔模型(二)沙漏模型GFEABCDABCDEFG①ADAEDEAFABACBCAG；②22:ADEABCSSAFAG△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方；⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具．在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．五年级.几何.五大模型五、共边定理（燕尾定理）有一条公共边的三角形叫做共边三角形。共边定理：设直线AB与PQ交于点M，则SPMPABSQMQAB特殊情况：当PQ∥AB时，易知△PAB与△QAB的高相等，从而S△PAB=S△QAB例题精讲一、三角形相似模型【例1】图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?101010五年级.几何.五大模型【考点】相似三角形模型【难度】4星【题型】解答【解析】如下图所示，为了方便所叙，将某些点标上字母，并连接BG．DCBAGxxxx101010设△AEG的面积为x，显然△EBG、△BFG、△FCG的面积均为x，则△ABF的面积为3x，120101002ABFS即1003x，那么正方形内空白部分的面积为40043x.所以原题中阴影部分面积为400800202033(平方厘米)．【答案】8003。【巩固】如图，四边形ABCD和EFGH都是平行四边形，四边形ABCD的面积是16，:3:1BGGC，则四边形EFGH的面积________．HGFEDCBA【考点】相似三角形模型【难度】3星【题型】填空【解析】因为FGHE为平行四边形，所以//ECAG，所以AGCE为平行四边形．:3:1BGGC，那么:1:4GCBC，所以1116444AGCEABCDSS．又AEGC，所以::1:3AEBGGCBG，根据沙漏模型，::3:1FGAFBGAE，所以334344FGHEAGCESS．【答案】3。【例2】已知三角形ABC的面积为a，:2:1AFFC，E是BD的中点，且EF∥BC，交CD于G，求阴影部分的面积．五年级.几何.五大模型ABCDEGF【考点】相似三角形模型【难度】4星【题型】解答【解析】已知:2:1AFFC，且EF∥BC，利用相似三角形性质可知::2:3EFBCAFAC，所以23EFBC，且:4:9AEFABCSS．又因为E是BD的中点，所以EG是三角形DBC的中位线，那么12EGBC，12::3:423EGEF，所以:1:4GFEF，可得:1:8CFGAFESS，所以:1:18CFGABCSS，那么18CFGaS．【答案】18a。【巩固】图中ABCD是边长为12cm的正方形，从G到正方形顶点C、D连成一个三角形，已知这个三角形在AB上截得的EF长度为4cm，那么三角形GDC的面积是多少？ABCDEFGNMABCDEFG【考点】相似三角形模型【难度】4星【题型】解答【解析】根据题中条件，可以直接判断出EF与D...