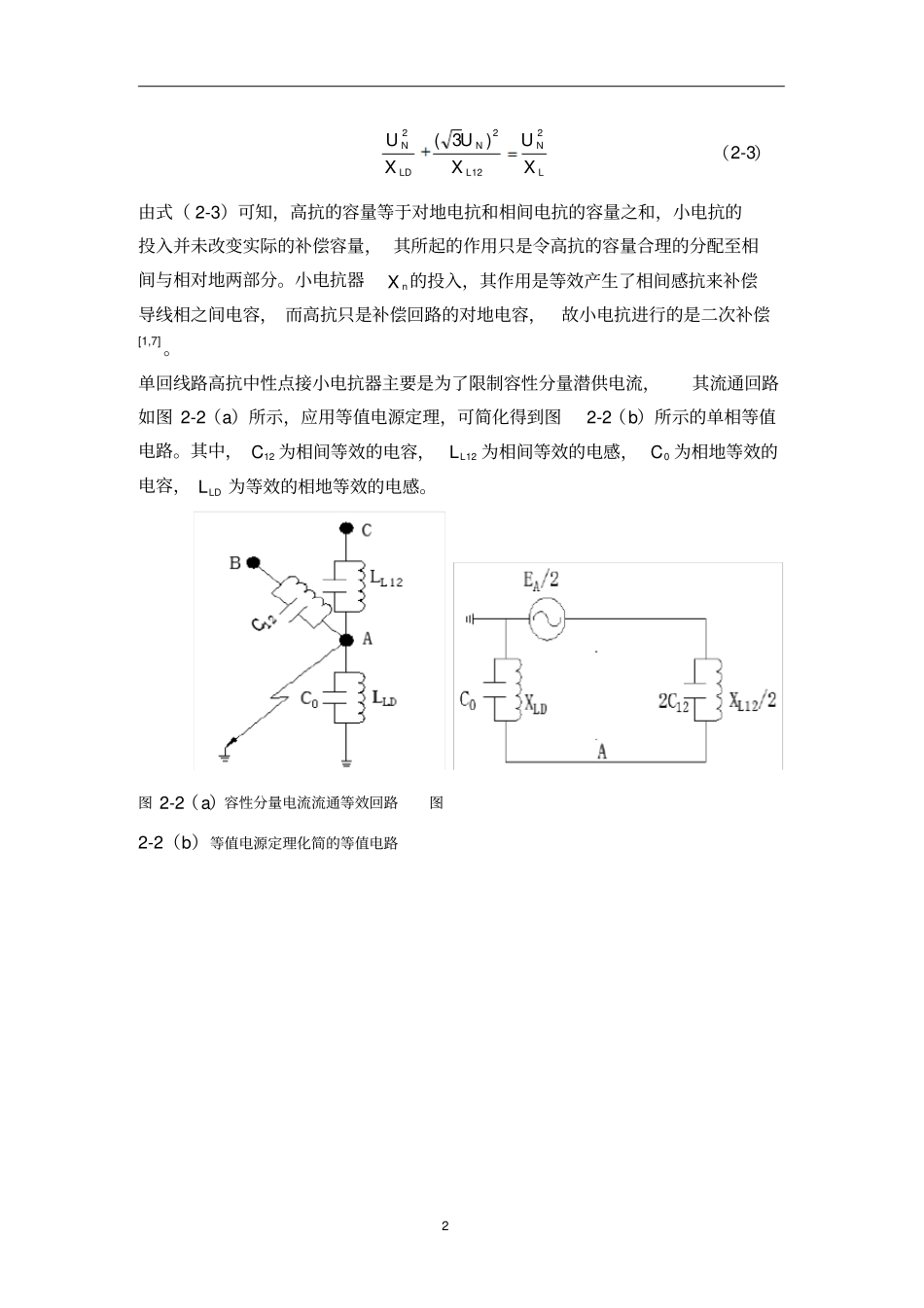
1并联高抗中性点小电抗补偿原理分析及参数选择方法并联高抗中性点接小电抗四线补偿的思想是通过对导线相间电容的补偿来隔离相间联系,削弱潜供电流与恢复电压的电容性分量,此时小电抗进行的是二次补偿。在系统不同的运行情况下,小电抗器参数选择的原则和方法也不相同。2.1等值电源定理分析小电抗二次补偿高抗中性点加小电抗四线补偿原理示意图见图1-4。高抗中性点经过小电抗器接地后的电路见图2-1(a)。LX为三相电感,nX为中性点单相电感。图2-1四线补偿系统等效电路图图2-1(a)所示的四线补偿系统经星-角变换得到图2-1(b)所示的系统等效电路。其中以上两种形式的电路参数满足如下关系nLLDXXX30LLLLLLXXXXXXXX0nn012393式中,0LX为小电抗接入前系统对地等效阻抗;LDX和12LX为小电抗接入后系统等效对地阻抗与相间阻抗。对于三相单相电抗器(LLXX0),则可变换为nLLDXXX3LnLLXXXX3/212通过式(12)和(22)可知高抗LX、对地阻抗LDX和相间阻抗12LX的容量存在以下等式关系。(2-1)(2-2)2LNLNLDNXUXUXU21222)3((2-3)由式(2-3)可知,高抗的容量等于对地电抗和相间电抗的容量之和,小电抗的投入并未改变实际的补偿容量,其所起的作用只是令高抗的容量合理的分配至相间与相对地两部分。小电抗器nX的投入,其作用是等效产生了相间感抗来补偿导线相之间电容,而高抗只是补偿回路的对地电容,故小电抗进行的是二次补偿[1,7]。单回线路高抗中性点接小电抗器主要是为了限制容性分量潜供电流,其流通回路如图2-2(a)所示,应用等值电源定理,可简化得到图2-2(b)所示的单相等值电路。其中,12C为相间等效的电容,12LL为相间等效的电感,0C为相地等效的电容,LDL为等效的相地等效的电感。图2-2(a)容性分量电流流通等效回路图2-2(b)等值电源定理化简的等值电路可以看出,欲要使接地通道流过的潜供电流为最小,则需使122C的阻抗值和2/12LX相等,使得线路的相间阻抗参数成开路状态,即使故障相(A相)的电压为零。由此可知12121CXL(2-4)其物理意义由图2-2(b)可以得出,即使线路相间等效的容抗12CX和四线补偿系统的相间等效感抗12LX组成并联谐振,线路相间趋于开路。将式(2-1)代入式(2-4)整理后得331L0LL122LnXXXCXX(2-5)此时导线相间电容被完全补偿,小电抗最大限度的促进了二次电弧的熄灭,限制了恢复电压。一般情况小电抗器最佳理论参数值均按对导线相间容抗近似有全补偿来设计[13]。若超高压线路的高抗由三个单相电感组成,则存在0LLXX,此时,式(2-5)可转化为L122Ln31XCXX(2-6)设并联高抗(高抗结构为三相单相电抗)的补偿度T,结合超高压正序、零序电容1C、0C的关系,则中性点小电抗值表示为3/13/1211121CTCTCCTCXXLn(2-7)其中,T为线路中并联电抗的补偿度,LCLXCQQT11;500kV全线正、零序、相间电容1C、0C、12C关系可表示为3/0112CCC。2.2对称分量法分析小电抗二次补偿使用对称分量法[5,14],分析图1-1可得,超高压系统非全相运行(A相断开),发生纵向故障时故障处的边界条件为0AI0CBUU式中,AI为通过A相上开关的电流,BU和CU分别为B、C两相开关之间电压。使用对称分量法分析,由式(2-8)可得使用序分量所表示的边界条件为0021III021UUU式中,1I、2I和0I分别为断线上的正、负和零序电流;1U、2U和0U分别为断口处对地的正、负和零电压。由式(2-9)可得如下图的系统发生A相断相时系统的复合序网图[14]。Z1、Z2和Z0分别为线路首端的三序阻抗,且有Z1=Z2。若将输电线路按集中式参数计算,即可等效为等值的正序容抗XC1与零序容抗XC0。图2-3A相断相时的系统复合序网电路图由图2-3可得,开断相A相对地电压为0101010102122XXXXEZZZZEUUUUAAA(2-10)式中,X1=XC1//XL1,X0=XC0//XL0;线路的等效电抗较容抗小得多,可忽略。当线路中加装有并联电抗器(01LL)时,由式(2-10)和C1与C0之间的关系可得此时开断相对地电压为1200120112012012323CCLLLLCLLLLEUAA(2-11)(2-8)(2-9)当式(2-11)中分母0,AU时,发生谐振。可得谐振条件为101202123LLCC(2-12)对于三相单相电抗器(01LL),谐振条件为1012012321CCCCL(2-13)由式(2-10)可知,若能使10LL,且001CL,则能...