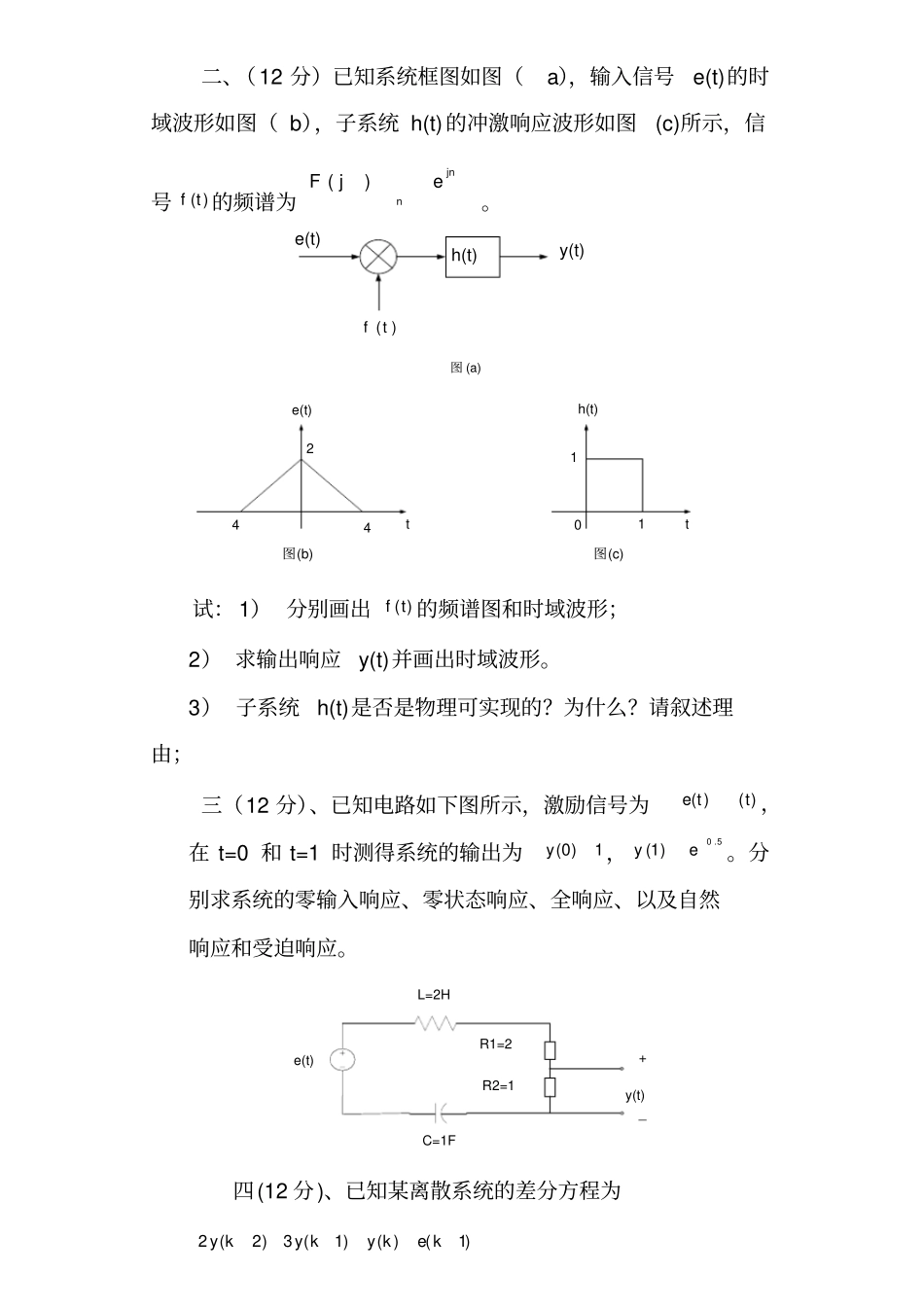
湖南工程学院考试卷(A、B卷)课程名称信号与系统考试学期得分适用专业电子信息工程考试形式闭卷考试时间长度120分钟一、简单计算题(每题8分):1、已知某连续信号()ft的傅里叶变换为21()23Fjj,按照取样间隔1T对其进行取样得到离散时间序列()fk,序列()fk的Z变换。2、求序列10()1,2,1kfk和2()1cos()2fkkk的卷积和。3、已知某双边序列的Z变换为21()1092Fzzz,求该序列的时域表达式()fk。4、已知某连续系统的特征多项式为:269111063)(234567ssssssssD试判断该系统的稳定情况,并指出系统含有负实部、零实部和正实部的根各有几个?5、已知某连续时间系统的系统函数为:3232642()21sssHssss。试给出该系统的状态方程。6、求出下面框图所示离散时间系统的系统函数。1z1z2-0.3)(ke)(kr-0.2二、(12分)已知系统框图如图(a),输入信号e(t)的时域波形如图(b),子系统h(t)的冲激响应波形如图(c)所示,信号()ft的频谱为()jnnFje。e(t)图(a)h(t)y(t))(tfe(t)244t图(b)h(t)t图(c)011试:1)分别画出)(tf的频谱图和时域波形;2)求输出响应y(t)并画出时域波形。3)子系统h(t)是否是物理可实现的?为什么?请叙述理由;三(12分)、已知电路如下图所示,激励信号为)()(tte,在t=0和t=1时测得系统的输出为1)0(y,5.0)1(ey。分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应。e(t)L=2HC=1FR1=2R2=1+y(t)_四(12分)、已知某离散系统的差分方程为)1()()1(3)2(2kekykyky其初始状态为6)2(,2)1(ziziyy,激励)()(kke;求:1)零输入响应)(kyzi、零状态响应)(kyzs及全响应)(ky;2)指出其中的自由响应分量和受迫响应分量;3)判断该系统的稳定性。五(12分)、已知某离散时间系统的单位函数响应()cos()2khkk。1)1)求其系统函数()Hz;2)2)粗略绘出该系统的幅频特性;3)3)画出该系统的框图。六、(10分)请叙述并证明z变换的卷积定理。参考答案:1、已知某连续信号()ft的傅里叶变换为21()23Fjj,按照取样间隔1T对其进行取样得到离散时间序列()fk,序列()fk的Z变换。解法一:f(t)的拉普拉斯变换为2111)2)(1(1321)(2sssssssF,2111)(Re)(ezzezzezzKezzsFszFniTsissnisTii解法二:f(t)=L1{F(jw)}=(ete2t)(t)f(k)=(eke2k)(k)=)())()((21keekkF(z)=Z[f(k)]=21ezzezz1、2、求序列10()1,2,1kfk和2()1cos()2fkkk的卷积和。解:f1(k)={1,2,1}=(k)+2(k1)+(k2)f1(k)*f2(k)=f2(k)+2f2(k1)+f2(k2)3、已知某双边序列的Z变换为21()1092Fzzz,求该序列的时域表达式()fk。解:5.014.01)(zzzF,两个单阶极点为0.4、0.5当收敛域为|z|>0.5时,f(k)=((0.4)k1(0.5)k1)(k1)当收敛域为0.4<|z|<0.5时,f(k)=(0.4)k1(k1)+(0.5)k1(k)当收敛域为|z|<0.4时,f(k)=(0.4)k1(k)+(0.5)k1(k)点评:此题应对收敛域分别讨论,很多学生只写出第一步答案,即只考虑单边序列。4、已知某连续系统的特征多项式为:269111063)(234567ssssssssD试判断该系统的稳定情况,并指出系统含有负实部、零实部和正实部的根各有几个?解构作罗斯-霍维茨阵列611617s291036s03168385s2314s342(00)32sss此时出现全零行,有辅助多项式34646,4,6ss求导可得以代替全零行系数。210322232sss由罗斯-霍维茨数列可见,元素符号并不改变,说明s右半平面无极点。再由42320ss令2sx则有2320xx可解得1,2x相应地有1,21sj3,42sj2这说明该系统的系统函数在虚轴上有四个单极点分别为土j及土j2,系统为临界稳定。所以系统含有三个负实部的根、四个零实部的根,无正实部的根。点评:此题得分率很低。很多学生对全零行不知如何处理。5、已知某连续时间系统的系统函数为:3232642()21sssHssss。试给出该系统的状态方程。解:系统的微分方程为)(2)(4)(6)()()()(2)(tetetetetytytyty取原来的辅助变量q及其各阶导数为状态变量并分别表示为1xq、2'xq、3''xq、''''3xq,于是,由此微分方程立即可以写出如下方程状态方程:)(2'''32133221texxxxxxxx输出方程:)(436423213213texxxxxxxy或者写成矩阵形式,上式即为exxxxxx100211010100'''321321BeAx``)(431321texxxyDeCx6、求出下面框图所示离散时间系统的系统函数。1z1z2-0.3)(ke)(kr-0.2解:06.05.03.22.01)3.02...