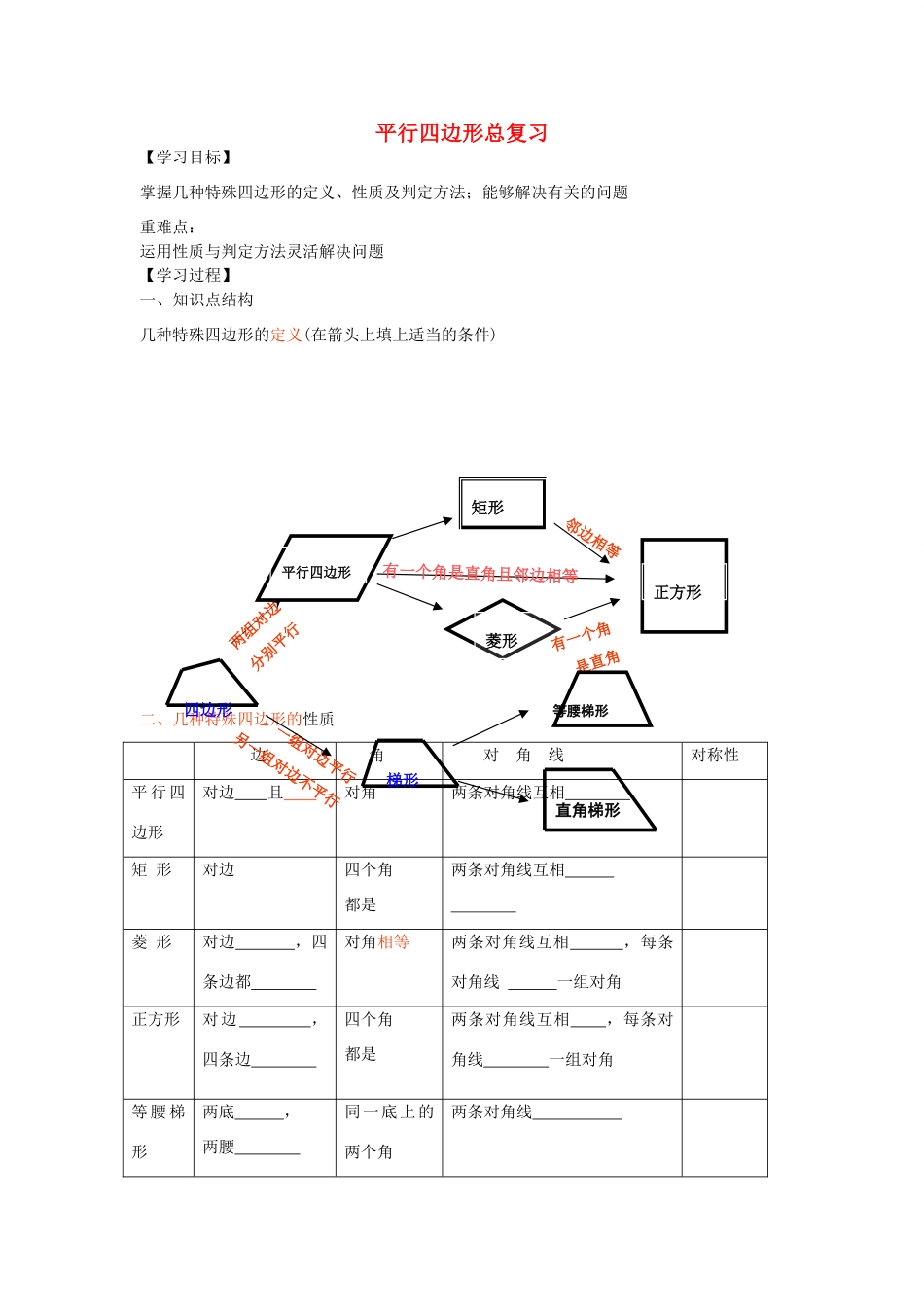
平行四边形总复习【学习目标】掌握几种特殊四边形的定义、性质及判定方法;能够解决有关的问题重难点:运用性质与判定方法灵活解决问题【学习过程】一、知识点结构几种特殊四边形的定义(在箭头上填上适当的条件)二、几种特殊四边形的性质边角对角线对称性平行四边形对边且对角两条对角线互相矩形对边四个角都是两条对角线互相菱形对边,四条边都对角相等两条对角线互相,每条对角线一组对角正方形对边,四条边四个角都是两条对角线互相,每条对角线一组对角等腰梯形两底,两腰同一底上的两个角两条对角线菱形两组对边分别平行邻边相等有一个角是直角一组对边平行另一组对边不平行四边形有一个角是直角且邻边相等平行四边形矩形正方形梯形等腰梯形直角梯形三、巩固练习1.平行四边形的对角线相等;()2.矩形的四个角都相等;()3.菱形的对角线互相垂直平分;()4.顺次连结四边形各边中点所得到的四边形一定是()(A)矩形。(B)正方形。(C)菱形。(D)平行四边形5.下列性质中,平行四边形不一定具备的是()(A)对角相等。(B)邻角互补。(C)对角互补。(D)内角和是360°6.正方形具有而菱形不一定具有的性质是()(A)对角线互相平分。(B)对角线相等。(C)对角线平分一组对角。(D)对角线互相垂直。7.平行四边形的两邻边分别为6和8,那么其对角线应()A.大于2,B.小于14C.大于2且小于14D.大于2或小于128.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于F.试确定AD与EF的位置关系,并说明理由.四、特殊四边形的常用判定方法平行四边形1、有两组的四边形是平行四边形。(定义)2、两组的四边形是平行四边形。(边)3、一组的四边形是平行四边形。4、的四边形是平行四边形(对角线)5、的四边形是平行四边形(角)1、有一个角是+=矩形(定义)2、有三个角是的四边形=矩形3、对角线的平行四边形=矩形AEBDCF12OABCDO图19-3矩形菱形1、+=菱形(定义)2、边都相等的四边形是菱形。3、对角线的平行四边形是菱形。正方形1、有一个角是且有一组的平行四边形是正方(定义)2、一组邻边相等+=正方形3、一角为90°+=正方形等腰梯形1、两相等的梯形(定义)2、在同一底上的两个角的梯形3、两条的梯形。五、其他重要定理1.三角形中位线定理:三角形的中位线_______三角形的第三边,且等于第三边的_______。2.在直角三角形中,斜边上的中线等于。3.在直角三角形中,30°角所对的直角边等于斜边的;六、课后作业1.如图19-3,正方形ABCD的对线AC、BD相交于点O.那么图中共有个等腰直角三角形.A.梯形B.等腰梯形C.直角梯形D.任意四边形4.已知ABCD是平行四边形,下列结论中不一定正确的是()A.AB=CDB.AC=BDC.当AC⊥BD时,它是菱形D.当∠ABC=90°时,它是矩形5.如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是()A.矩形B.菱形C.正方形D.菱形、矩形或正方形6.已知:在梯形ABCD中,AD//BC,E为BC中点,EF⊥AB,EG⊥CD,EF=EG。求证:梯形ABCD为等腰梯形?ABCDE