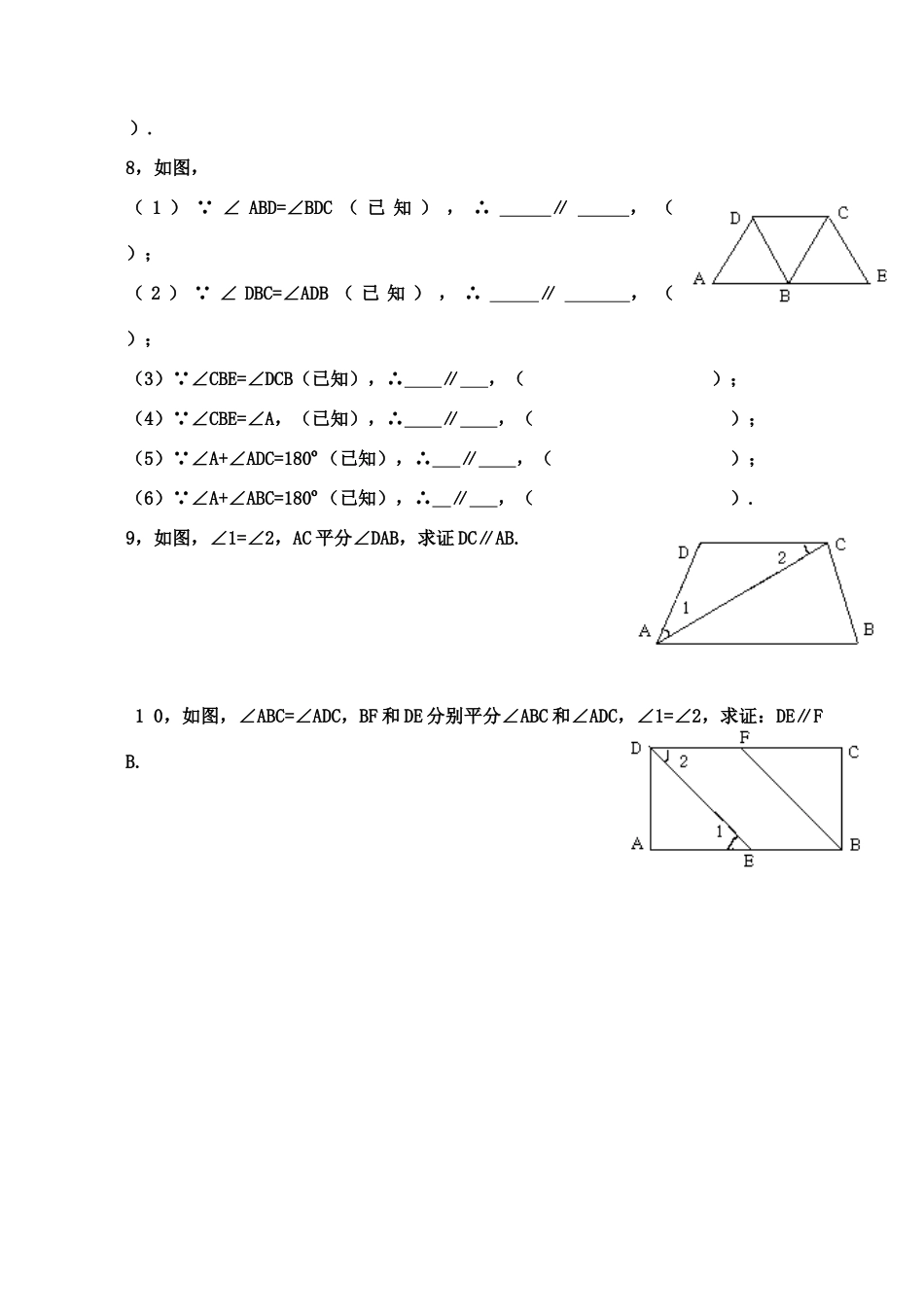
6.3为什么它们平行一、【温故】前面我们探索过直线平行的条件.两条直线在什么情况下互相平行二、【知新】探究一:求证:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行定理可简单地写成探究二:求证:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行这一定理可以简单说成:刚才我们是应用判定定理“同旁内角互补,两直线平行”来证明这一定理的.下面大家来想一想借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论呢?已知,如图,直线a⊥c,b⊥c.求证:a∥b.证明:∵a⊥c,b⊥c(已知)∴∠1=90°∠2=90°()∴∠1=∠2(等量代换)∴b∥a()由此可以得到:“如果两条直线都和第三条直线垂直,那么这两条直线平行”的结论.【三】达标:1,下列说法错误的是()A、同位角不一定相等B、内错角都相等C、同旁内角可能相等D、同旁内角互补则两直线平行2,在同一平面内,直线与两条平行线a,b的位置关系是()A.一定与a,b都平行B.可能与a平行,与b相交C.一定与a,b都相交D.与a,b都平行或都相交3,四边形ABCD中,若∠B+∠C=180º,则AB与CD的关系是()A.相交B.平行C.垂直D.垂合4,同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是()A.1个B.2个C.3个D.4个5,如图,下列条件能证明AD∥BC的是()A.∠A=∠CB.∠B=∠DC.∠B=∠CD.∠A+∠B=180º6,如图,直线AB,CD与EF相交于G,H,下列条件:①∠1=∠2;②∠3=∠6;③∠2=∠8;④∠5+∠8=180º,其中能判定AB∥CD的是()A.①③B.①②④C.①③④D.②③④7(1)∵∠1=∠A(已知)∴∥,();(2)∵∠3=∠4(已知),∴∥,();(3)∵∠2=∠5(已知),∴∥,();(4)∵∠ADC+∠C=180(已知),∴∥,().8,如图,(1)∵∠ABD=∠BDC(已知),∴∥,();(2)∵∠DBC=∠ADB(已知),∴∥,();(3)∵∠CBE=∠DCB(已知),∴∥,();(4)∵∠CBE=∠A,(已知),∴∥,();(5)∵∠A+∠ADC=180º(已知),∴∥,();(6)∵∠A+∠ABC=180º(已知),∴∥,().9,如图,∠1=∠2,AC平分∠DAB,求证DC∥AB.10,如图,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠1=∠2,求证:DE∥FB.