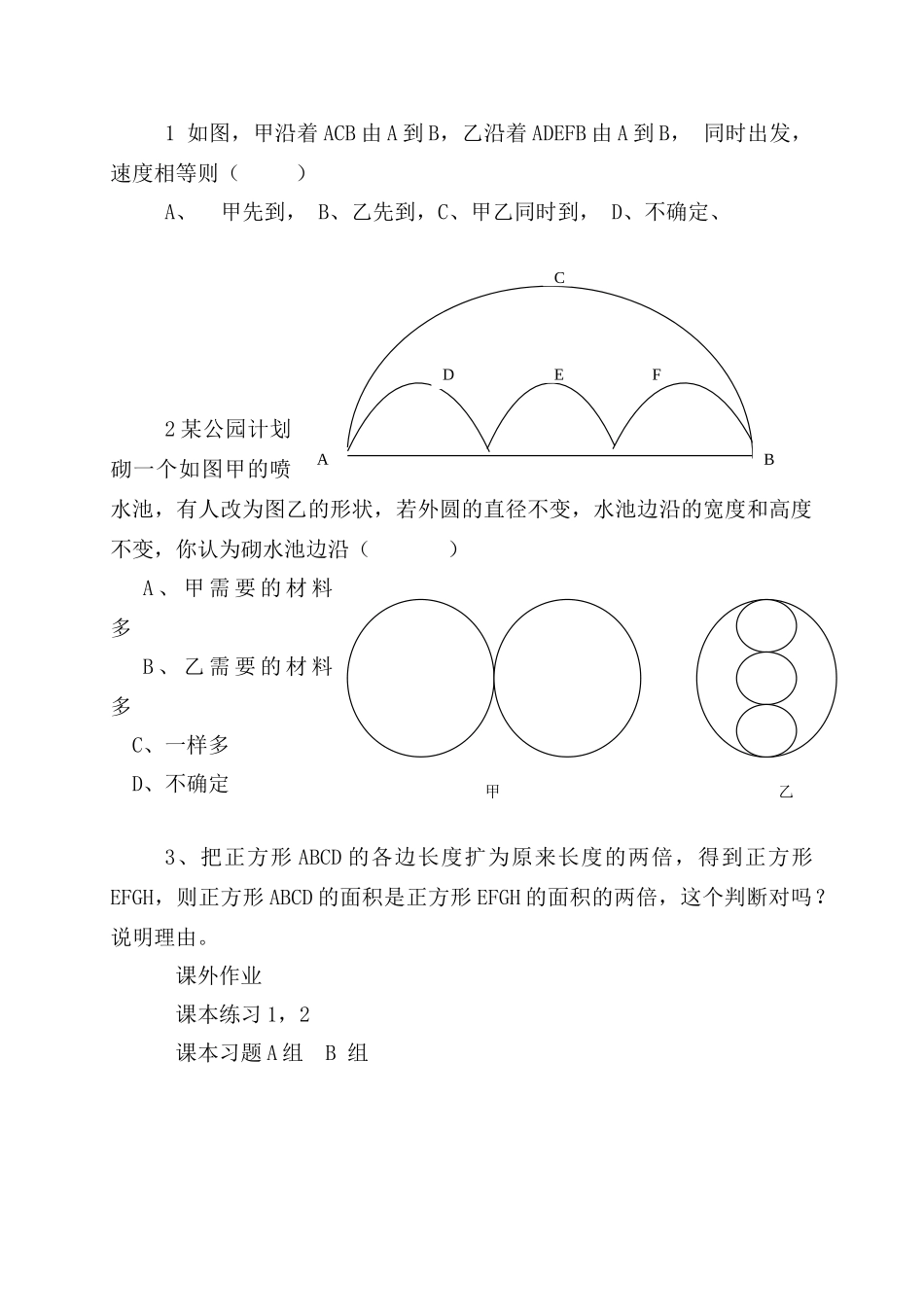
11.2《为什么要证明》导学案课本内容P117-P118页内容课前准备圆规刻度尺学习目标通过本节课的学习让学生明白由观察,实验,归纳和类比得到的命题仅仅是一种猜想,未必都是真命题,需要通过推理的方法加以证实。学习过程一、学生自主学习课本P117-P118页内容二预习检测1、下列命题是人们利用观察,实验,归纳和类比得到的。判断是否是真命题(1)两点之间,线段最短。()(2)n边形有条对角线.()(3)对顶角相等。()2、思考:观察,实验,归纳和类比是我们发现规律,获取结论的重要方法,用这些方法得到的结论一定正确吗?答:()3(1)小亮通过计算发现,当n=1,2,3,4,5时,代数式n+3n+1的值是质数,于是得出结论,当n为正整数时,n+3n+1的值一定是质数,试举例证明,这个结论是正确的。(2)小营在学习根式时,从乘法满足分配律,类比得到=,试举例说明这个结论是错误的。三小组交流收获:为什么要证明?答:四练习1、先观察再比较线段AB与线段CD的长短。2、图中AB是直线还是折线?3、用直尺验证线段d与在一条直线上。五、拓展:1、对于多项式,当时,;当时,;当时,。由此断定,时,,这个判断对吗?为什么?2、由幂的乘方运算性质得:、、、、、、、、,类比上述等式,可得、、、、、、、、、,这个结论正确吗?请说明理由。六当堂测试ABABCDCD图1AB图2abcd图3甲乙ABCDEF1如图,甲沿着ACB由A到B,乙沿着ADEFB由A到B,同时出发,速度相等则()A、甲先到,B、乙先到,C、甲乙同时到,D、不确定、2某公园计划砌一个如图甲的喷水池,有人改为图乙的形状,若外圆的直径不变,水池边沿的宽度和高度不变,你认为砌水池边沿()A、甲需要的材料多B、乙需要的材料多C、一样多D、不确定3、把正方形ABCD的各边长度扩为原来长度的两倍,得到正方形EFGH,则正方形ABCD的面积是正方形EFGH的面积的两倍,这个判断对吗?说明理由。课外作业课本练习1,2课本习题A组B组