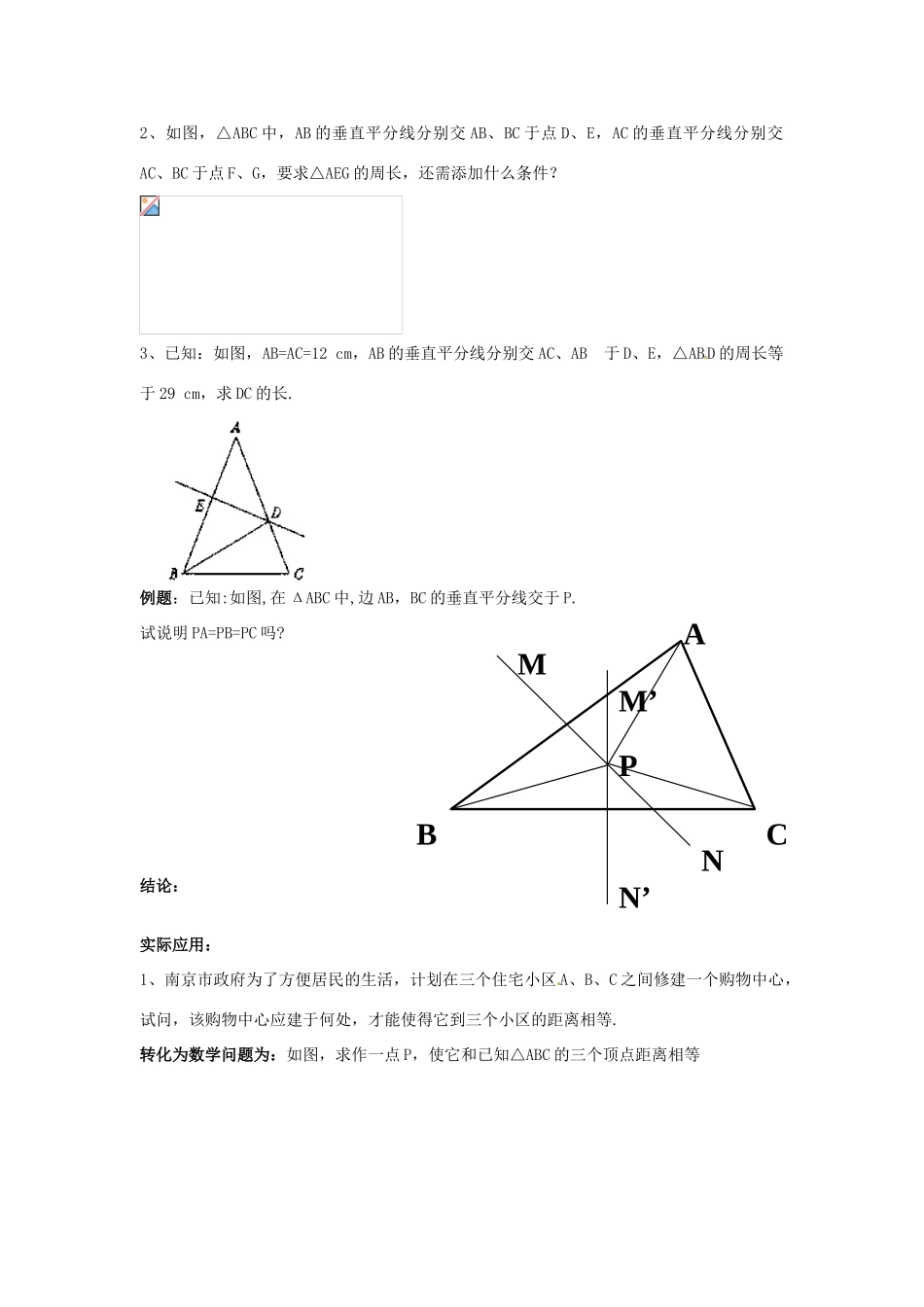
16.2线段的垂直平分线学习目标1、让学生经历线段的折叠过程探索线段的对称性,掌握中垂线的性质和判定方法;2、使学生会运用线段垂线的性质解决生活中的相关问题;3、培养学生动手探索的科学习惯。4、在“操作—探究—归纳—说理”的过程中学会有条理地思考和表达提高演绎推能力。学习重点线段中垂线的性质和判定学习难点发现线段中垂线的性质,线段中垂线的性质和判定学习过程一、创设情境:南京市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。二、动手实践,探索性质:问题1:线段是轴对称图形吗?为什么?问题2:按要求对折线段后,你发现折痕与线段有什么关系?问题3:按要求第二次对折线段后,你发现折痕上任一点到线段两端点的距离有什么关系?得出结论:课堂练习:1、如图,△ABC中边BC的中垂线交AB于点D,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪条线段的长?2、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,要求△AEG的周长,还需添加什么条件?3、已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于29cm,求DC的长.例题:已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.试说明PA=PB=PC吗?结论:实际应用:1、南京市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等.转化为数学问题为:如图,求作一点P,使它和已知△ABC的三个顶点距离相等BACMNM’N’P2、在312国道L(昆—沪段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?转化为数学问题为:如图,在直线L上求作一点P,使PA=PB总结反思:作业设计:班级姓名学号等第一、选择题1.如果三角形两边的垂直平分线的交点恰好落在第三边上,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形2.如图,AC=AD,BC=BD,则()A.CD垂直平分ADB.AB垂直平分CDC.CD平分∠ACBD.以上结论均不对第2题第3题3.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()A.BC>PC+APB.BC<PC+APC.BC=PC+APD.BC≥PC+AP二、填空题4.如图,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10cm,则BD=__________cm;若PA=10cm,则PB=__________cm.5.在△ABC中,AB、AC的垂直平分线相交于点P,则PA、PB、PC的大小关系是.6.如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12cm,AC=5cm,则AB+BD+AD=________cm,AB+BD+DC=__________cm,△ABC的周长是__________cm.答案1.B2.B3.C4.5,105.PA=PB=PC6.12,12,17第4题第6题