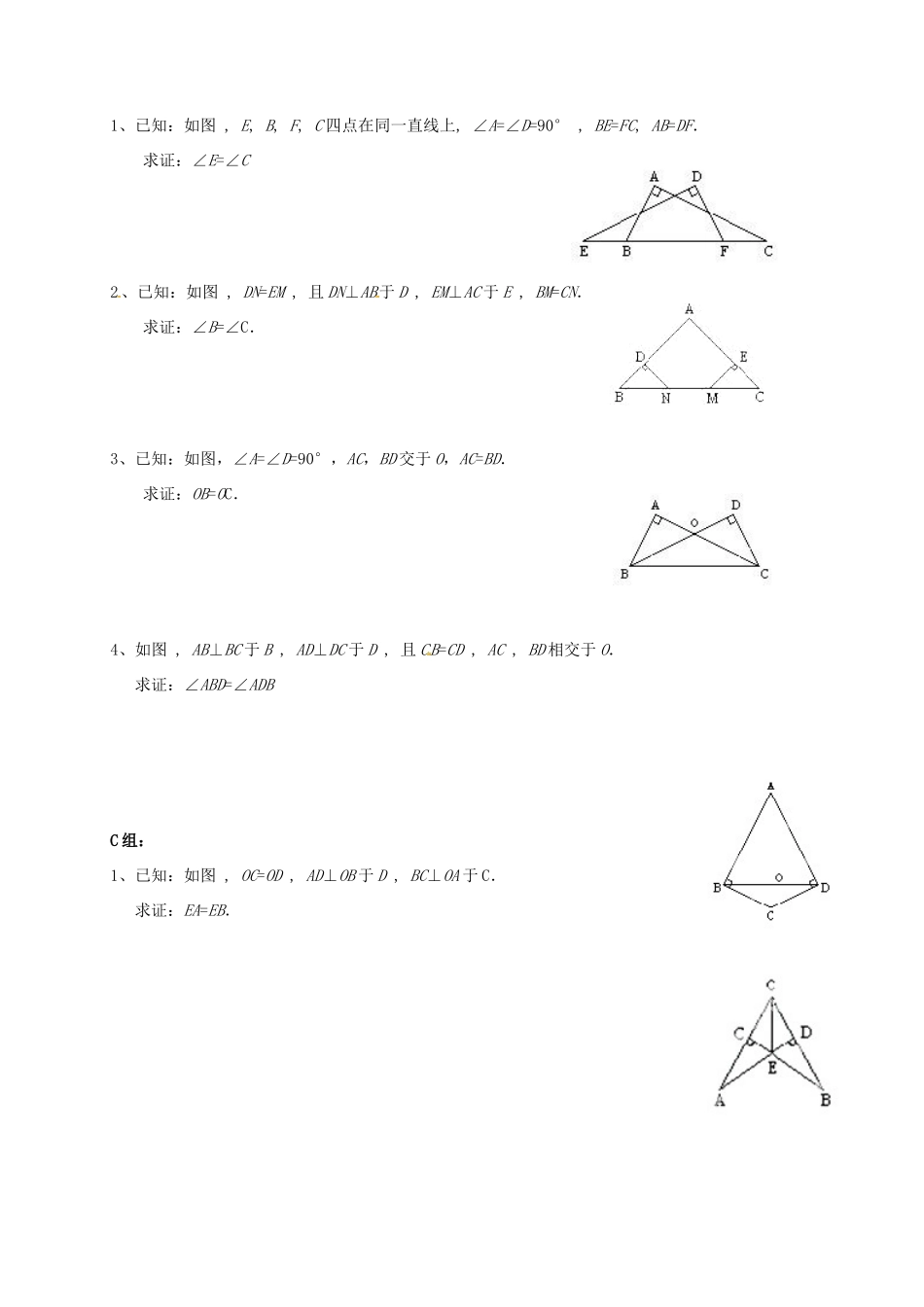
直角三角形(二)学习目标:会证明直角三角形全等的“HL”的判定定理,会利用“HL’’定理解决实际问题思考题:“HL”的判定定理具体内容是什么?怎样证明呢?问题与题例:问题1:证明:“在两个直角三角形中,直角所对的边即斜边和一条直角边对应相等的两个直角三角形全等.”问题2:你能用三角尺平分一个已知角吗?请同学们用手中的三角尺操作完成,并说明理由?问题3:已知∠ACB=∠BDA=90°,要使△ACB≌BDA,还需要什么条件?把它们分别写出来.目标检测:1、课本23页随堂练习2、如图,在△ABC≌△A'B'C'中,CD,C'D'分别分别是高,并且AC=A'C',CD=C'D'.∠ACB=∠A'C'B'.配餐练习:A组:如图,下面条件中,不能证出Rt△ABC≌Rt△A'B'C'的是________A.AC=A'C',BC=B'C'B.AB=A'B',AC=A'C'C.AB=B'C',AC=A'C'D.∠B=∠B',AB=A'B'2、已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=∠C3、已知:如图,CE⊥AB于E,BF⊥CD于F,且BF=CE.求证:BE=CF.B组:'CCADB'''BDA1、已知:如图,E,B,F,C四点在同一直线上,∠A=∠D=90°,BE=FC,AB=DF.求证:∠E=∠C2、已知:如图,DN=EM,且DN⊥AB于D,EM⊥AC于E,BM=CN.求证:∠B=∠C.3、已知:如图,∠A=∠D=90°,AC,BD交于O,AC=BD.求证:OB=OC.4、如图,AB⊥BC于B,AD⊥DC于D,且CB=CD,AC,BD相交于O.求证:∠ABD=∠ADBC组:1、已知:如图,OC=OD,AD⊥OB于D,BC⊥OA于C.求证:EA=EB.