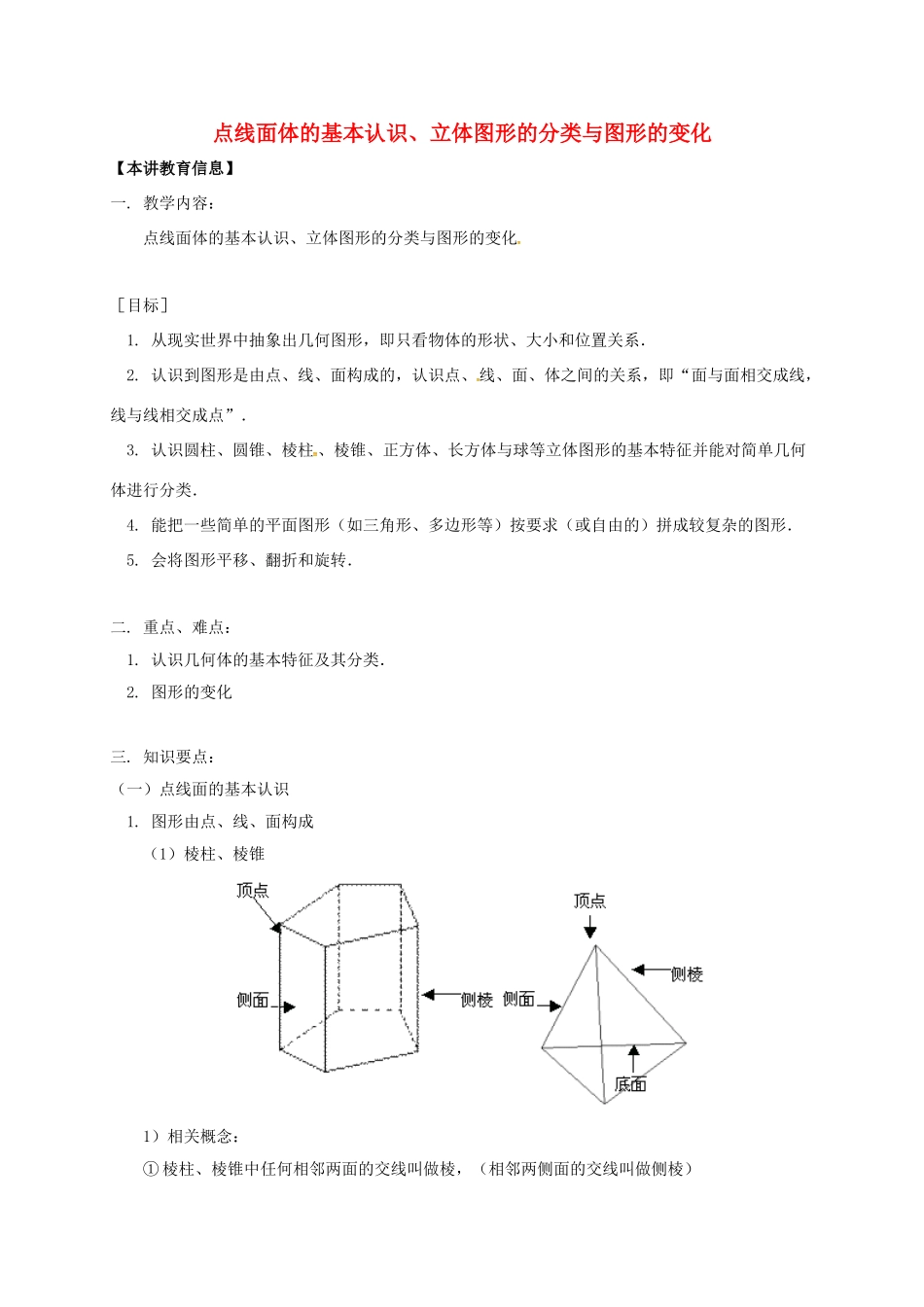
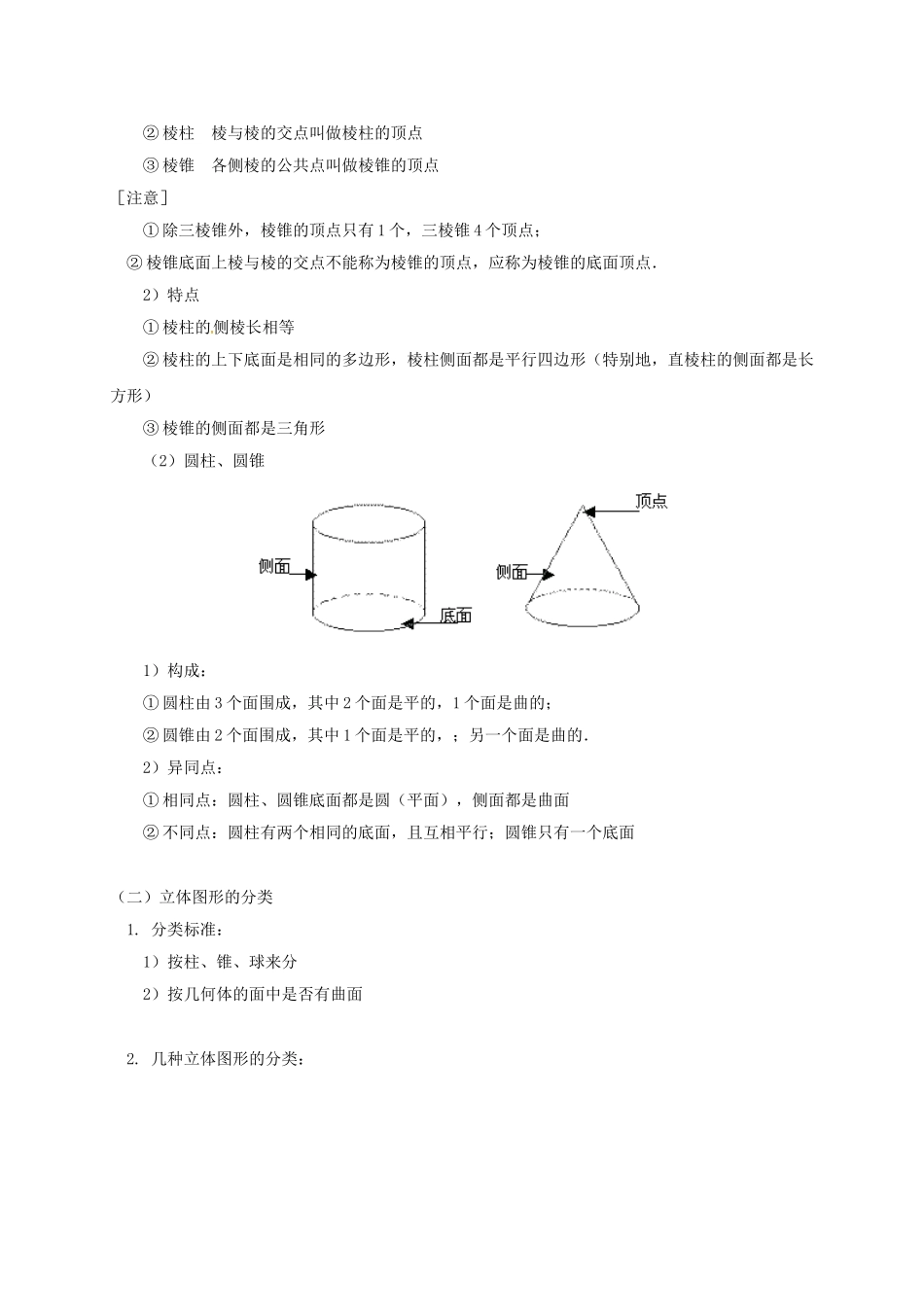
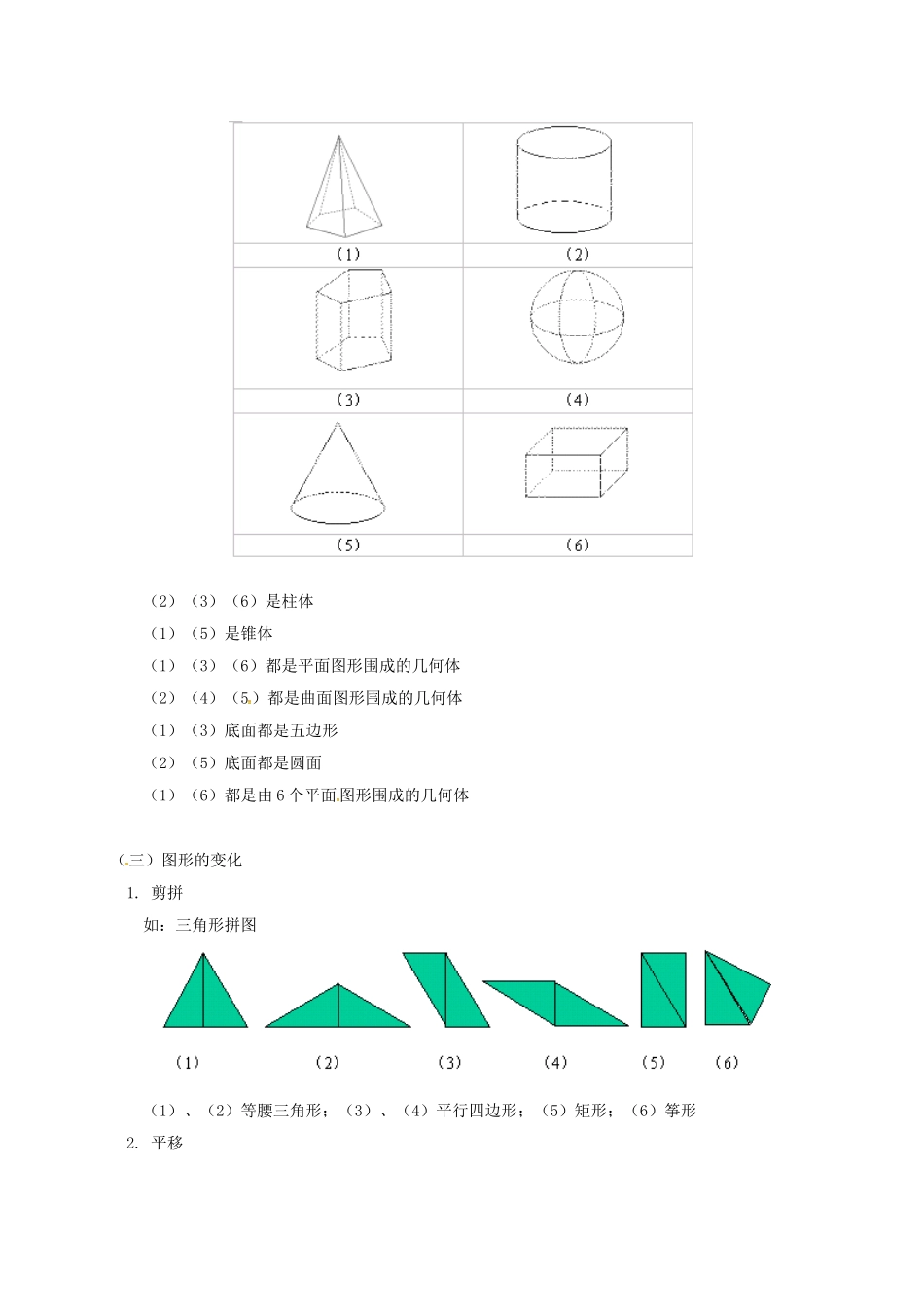
点线面体的基本认识、立体图形的分类与图形的变化【本讲教育信息】一.教学内容:点线面体的基本认识、立体图形的分类与图形的变化[目标]1.从现实世界中抽象出几何图形,即只看物体的形状、大小和位置关系.2.认识到图形是由点、线、面构成的,认识点、线、面、体之间的关系,即“面与面相交成线,线与线相交成点”.3.认识圆柱、圆锥、棱柱、棱锥、正方体、长方体与球等立体图形的基本特征并能对简单几何体进行分类.4.能把一些简单的平面图形(如三角形、多边形等)按要求(或自由的)拼成较复杂的图形.5.会将图形平移、翻折和旋转.二.重点、难点:1.认识几何体的基本特征及其分类.2.图形的变化三.知识要点:(一)点线面的基本认识1.图形由点、线、面构成(1)棱柱、棱锥1)相关概念:①棱柱、棱锥中任何相邻两面的交线叫做棱,(相邻两侧面的交线叫做侧棱)②棱柱棱与棱的交点叫做棱柱的顶点③棱锥各侧棱的公共点叫做棱锥的顶点[注意]①除三棱锥外,棱锥的顶点只有1个,三棱锥4个顶点;②棱锥底面上棱与棱的交点不能称为棱锥的顶点,应称为棱锥的底面顶点.2)特点①棱柱的侧棱长相等②棱柱的上下底面是相同的多边形,棱柱侧面都是平行四边形(特别地,直棱柱的侧面都是长方形)③棱锥的侧面都是三角形(2)圆柱、圆锥1)构成:①圆柱由3个面围成,其中2个面是平的,1个面是曲的;②圆锥由2个面围成,其中1个面是平的,;另一个面是曲的.2)异同点:①相同点:圆柱、圆锥底面都是圆(平面),侧面都是曲面②不同点:圆柱有两个相同的底面,且互相平行;圆锥只有一个底面(二)立体图形的分类1.分类标准:1)按柱、锥、球来分2)按几何体的面中是否有曲面2.几种立体图形的分类:(2)(3)(6)是柱体(1)(5)是锥体(1)(3)(6)都是平面图形围成的几何体(2)(4)(5)都是曲面图形围成的几何体(1)(3)底面都是五边形(2)(5)底面都是圆面(1)(6)都是由6个平面图形围成的几何体(三)图形的变化1.剪拼如:三角形拼图(1)、(2)等腰三角形;(3)、(4)平行四边形;(5)矩形;(6)筝形2.平移由一个图形改变为另一个图形,在改变的过程中,原图形上所有的点都沿同一个方向运动,且运动相等的距离.这样的图形改变叫做图形的平移变换.3.旋转(1)由一个图形改变为另一个图形,在改变的过程中,原图形上的所有点都绕一个固定的点或一条线,按同一个方向,转动同一个角度,这样的图形改变叫做图形的旋转变换.(2)点动成线,线动成面,面动成体4.翻折如下图(1)到(2)【典型例题】例1.在下列两行图形中,分别找出相互对应的图解:如下图:例2.下列图形都是由半圆经过变化而得到的,请说出它们最简单的变化过程.答:图(1)是先沿AB翻转,再沿AB平移;图(2)是以MN为轴翻转;图(3)是以O为中心旋转180°.例3.将以下方格图图(1)中阴影图形围绕点O,按顺时针方向依次旋转90°,看看会得到什么图形?(1)(2)分析:找准关键点的位置.答:如图(2).说明:旋转中图形的形状、大小与原图相同.通过平移、旋转、翻转可以得到很多美丽的图案,而变化前后仅仅是图形位置变化,形状、大小不变.例4.小明用如下左图的胶滚沿从左到右的方向将图案滚涂到墙上,右边所给的四个图案中符合胶滚的图案的是()答:选C.例5.适当地剪几刀,可以把图中的十字变成一个正方形,有人说用两刀就可以,你试试看.解:剪法如下图所示:例6.由平的面围成的立体图形又叫做多面体,有几个面,就叫做几面体.三棱锥有四个面,所以三棱锥又叫四面体;正方体又叫做六面体,有五条侧棱的棱柱又叫做七面体.(1)探索:如果把一个多面体的顶点数记为V,棱数记为E,面数记为F,填表:多面体VFEV+F–E四面体长方体五棱柱(2)猜想:由上面的探究你能得到一个什么结论?(3)验证:在课本的插图中再找出一个多面体,数一数它有几个顶点,几条棱,几个面,看看面数、顶点数、棱数还是否满足上述关系.(4)应用:(2)的结果对所有的多面体都成立,伟大的数学家欧拉证明了这个关系式,上述关系式叫做欧拉公式.根据欧拉公式,想一想会不会有一个多面体,它有10个面,30条棱,20...