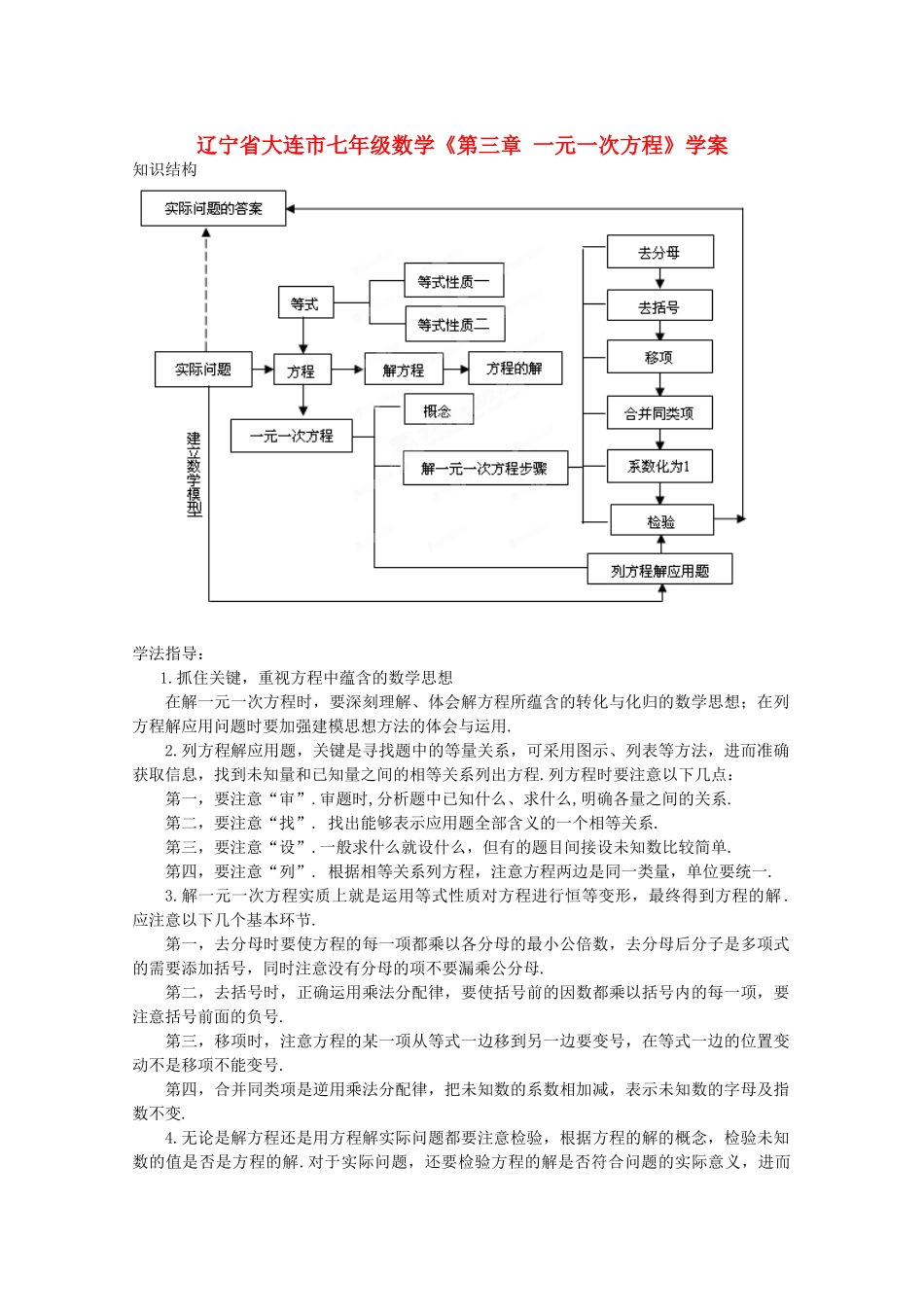
辽宁省大连市七年级数学《第三章一元一次方程》学案知识结构学法指导:1.抓住关键,重视方程中蕴含的数学思想在解一元一次方程时,要深刻理解、体会解方程所蕴含的转化与化归的数学思想;在列方程解应用问题时要加强建模思想方法的体会与运用.2.列方程解应用题,关键是寻找题中的等量关系,可采用图示、列表等方法,进而准确获取信息,找到未知量和已知量之间的相等关系列出方程.列方程时要注意以下几点:第一,要注意“审”.审题时,分析题中已知什么、求什么,明确各量之间的关系.第二,要注意“找”.找出能够表示应用题全部含义的一个相等关系.第三,要注意“设”.一般求什么就设什么,但有的题目间接设未知数比较简单.第四,要注意“列”.根据相等关系列方程,注意方程两边是同一类量,单位要统一.3.解一元一次方程实质上就是运用等式性质对方程进行恒等变形,最终得到方程的解.应注意以下几个基本环节.第一,去分母时要使方程的每一项都乘以各分母的最小公倍数,去分母后分子是多项式的需要添加括号,同时注意没有分母的项不要漏乘公分母.第二,去括号时,正确运用乘法分配律,要使括号前的因数都乘以括号内的每一项,要注意括号前面的负号.第三,移项时,注意方程的某一项从等式一边移到另一边要变号,在等式一边的位置变动不是移项不能变号.第四,合并同类项是逆用乘法分配律,把未知数的系数相加减,表示未知数的字母及指数不变.4.无论是解方程还是用方程解实际问题都要注意检验,根据方程的解的概念,检验未知数的值是否是方程的解.对于实际问题,还要检验方程的解是否符合问题的实际意义,进而确定它是否是实际问题的答案.3.1从算式到方程第一课时典例精析例1下列各式哪些是方程?①;②4+8=12;③;④;⑤;⑥;⑦;⑧.分析:用方程的定义入手,看各式是否满足方程的定义.解:①④⑤⑦⑧是方程.点拨:方程的判断必须满足两点:一是等式;二是含有未知数,二者缺一不可.例2根据下列条件列出方程(1)的比它的相反数小;(2)的平方的减去等于的3倍加1;分析:正确分析题意,用已知量和未知量建立相等关系.解:(1),(2).点拨:理解“相反数”“平方”的含义,“等于”、“比×××大”、“比×××小”“增加”“增加到”等是表示相等关系的常用词语.随堂练习1.下列各式是方程的是()A.B.3+5=8C.D.2.若比某数的相反数大2的数是8,设某数为,可列方程为()A.B.C.D.3.若单项式3acx+2与-7ac2x-1是同类项,可以得到关于x的方程为.4.列方程表示:的2倍与10的和等于18.5.一个两位数,十位上的数字为,个位数字比大2,且十位上的数与个位上的数的和为6,列方程为.6.课后演练1.下列四个式子中是方程的有()①;②;③;④1+2=3A.1个B.2个C.3个D.4个2.某校长方形的操场周长为210m,长与宽之差为15m,设宽为m,列方程为.3.的10%与的差比的2倍少3,列方程为.4.一件衣服打8折后,售价为88元,设原价为元,可列方程为.*5.把一个长方形分成如图3-1-1所示的7个小长方形,且这7个小长方形能完全重合,已知大长方形的宽为14cm,设小长方形的宽为cm,列方程为.第二课时典例精析例足球的表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块的数目比14cm图3-1-1为3:5,一个足球的表面一共有32个皮块,黑色皮块和白色皮块各有多少?分析:(1)设白色皮块有个,则黑色皮块有(32-x)个,黑色皮块与白色皮块的数目比为3:5,即为.由此列出方程.填写表3-1-1:由此发现上述方程的解为=.(2)设黑色皮块有3个,黑色皮块与白色皮块的数目比为3:5,则白色皮块有5x个,一个足球的表面共有个皮块(用含x的代数式表示),即32个皮块,由此列方程.填写表3-1-2:由此发现上述方程的解为=,黑色皮块有个,白色皮块有个.由于所设的未知数不同,(1)、(2)中两个方程完全不相同.只含有一个未知数,并且未知数的指数都是1的方程叫做方程.(1)分母中含有未知数的方程=不是一元一次方程,而(2)中是一元一次方程.理解方程的解的意义及一元一次方程的概念是关键.解:(1)=;;;;;20.(2);;8;16;24;32;40;48;4;12;20;一元一次.点拨:检验方程的解的方法:①将未知数的值分别代入方程的左右两边;②分别计算方程左右两边的值...