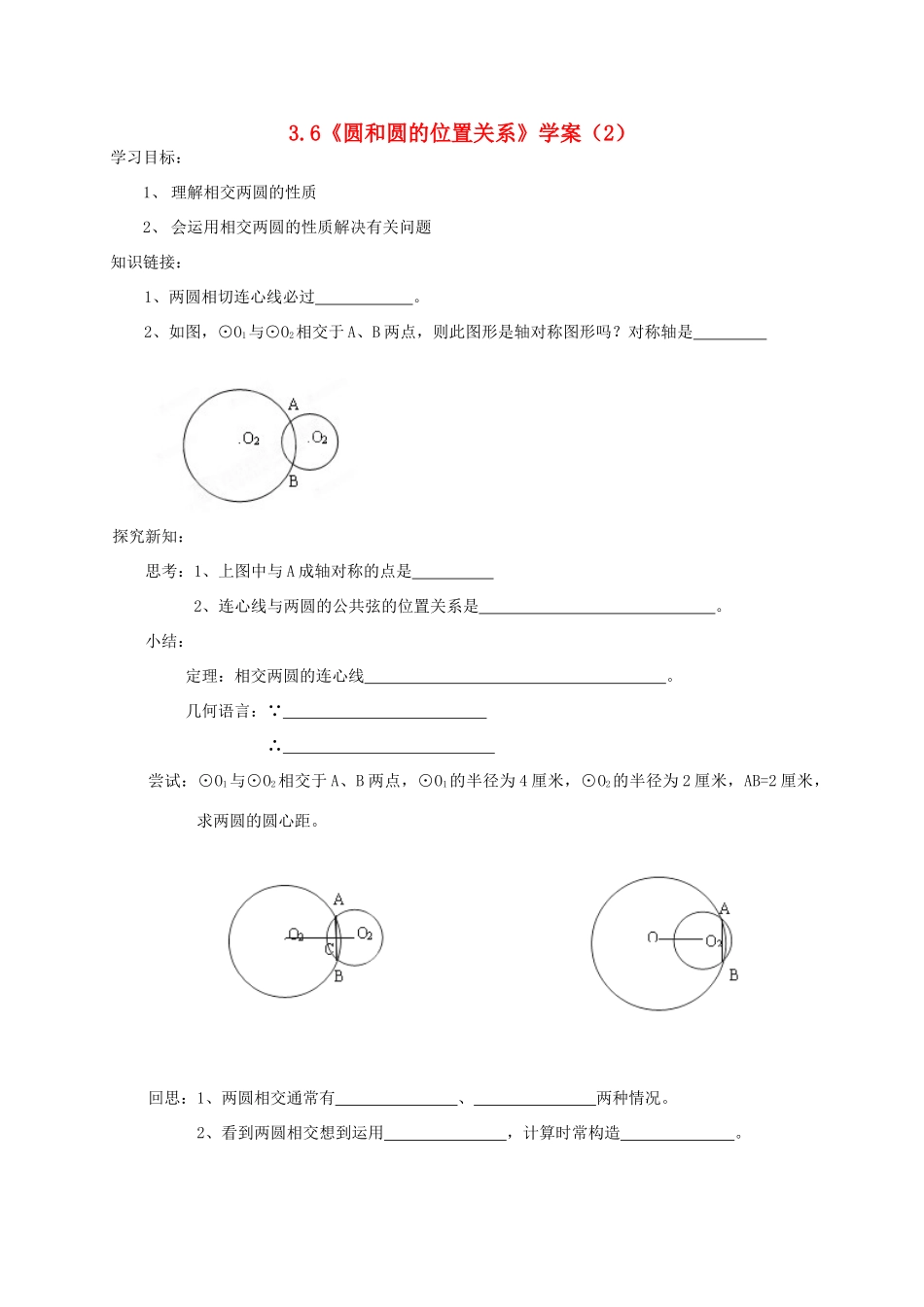
3.6《圆和圆的位置关系》学案(2)学习目标:1、理解相交两圆的性质2、会运用相交两圆的性质解决有关问题知识链接:1、两圆相切连心线必过。2、如图,⊙O1与⊙O2相交于A、B两点,则此图形是轴对称图形吗?对称轴是探究新知:思考:1、上图中与A成轴对称的点是2、连心线与两圆的公共弦的位置关系是。小结:定理:相交两圆的连心线。几何语言:∵∴尝试:⊙O1与⊙O2相交于A、B两点,⊙O1的半径为4厘米,⊙O2的半径为2厘米,AB=2厘米,求两圆的圆心距。回思:1、两圆相交通常有、两种情况。2、看到两圆相交想到运用,计算时常构造。巩固练习:1、已知半径为5厘米的两个等圆相交,公共弦长为6厘米,求两圆的圆心距。2、如图,⊙O1与⊙O2相交于A、B两点,且AO1,AO2分别是两圆的切线,A是切点,AO1=3厘米,AO2=4厘米,求AB的长。灵活运用:1、⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于D,连接AD。求证:(1)、AD是⊙O2的直径(2)、DA=DC友情提示:两圆相交时公共弦起桥梁作用,将两圆的角联系起来。2、如图,已知两个等圆⊙O1与⊙O2相交于A、B两点,⊙O1经过点O2。(1)、判断四边形O1AO2B的形状,并加以证明。(2)、求∠AO1B的度数。回顾反思:1、两圆相交。BO2O1A2、两圆相交常填加的辅助线是、