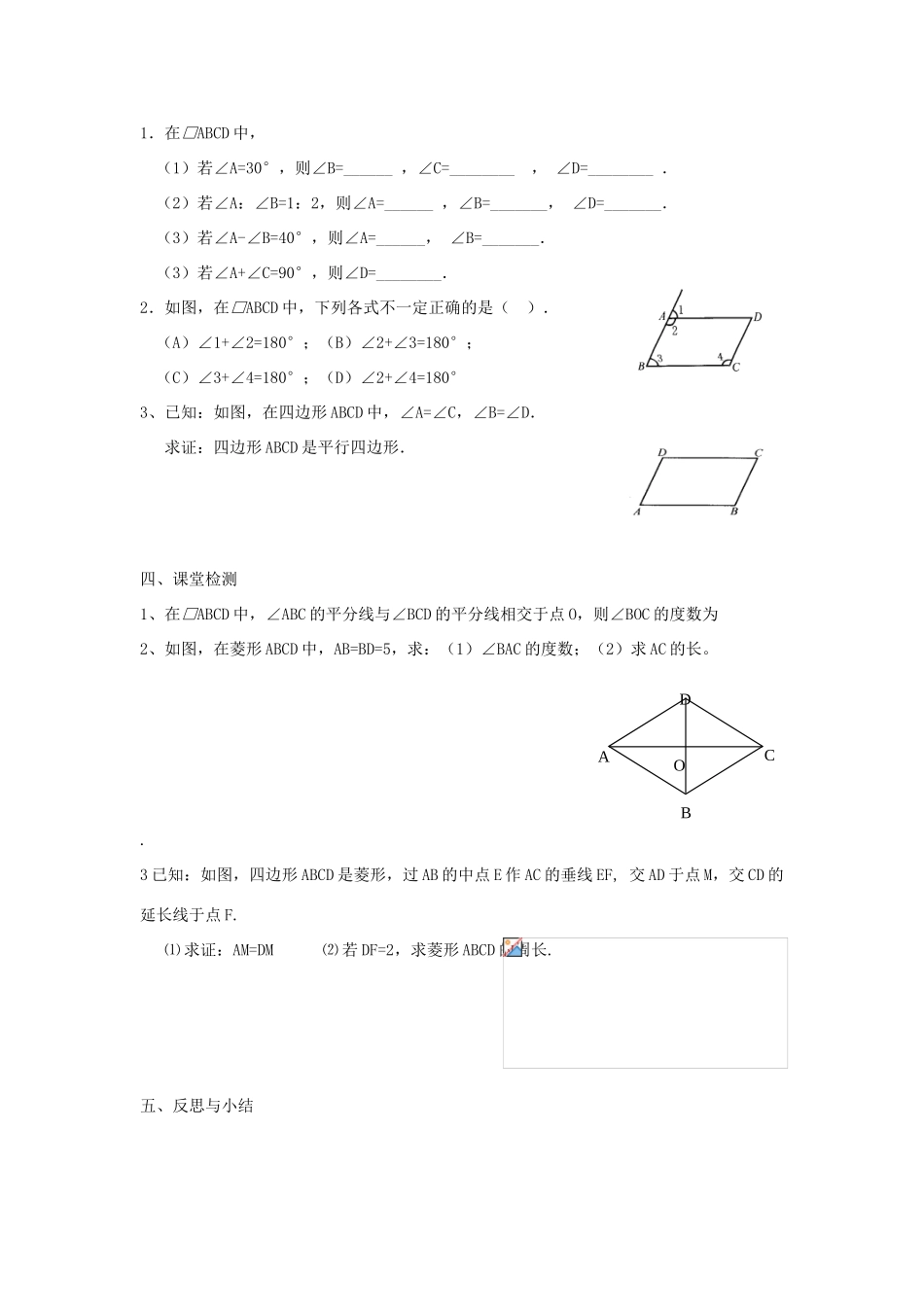
第19章:四边形复习教学目标:1、掌握特殊四边形的判定及其性质,能灵活运用特殊四边形的知识解一些实际问题.2、通过观察、猜想、验证、推理、交流等数学活动进一步发展学生的演绎推理能力和发散思维能力.3、经历探索二次函数相关题目的过程,体会数形结合思想、化归思想在数学中的广泛应用,同时感受数学知识来源于实际生活,反之,又服务于实际生活.重点:特殊四边形的判定及其性质,应用特殊四边形的知识分析和解决简单的实际问题.难点:特殊四边形性质的灵活运用,能把相关应用问题转化为数学问题.教学过程:一、知识回顾梳理本章的知识点:(从图形的定义、性质、判定、面积等方面考虑)二、课堂展示例1如图,在□ABCD中,已知AE,CF分别是∠DAB,∠BCD的角平分线.你认为四边形AFCE是平行四边形吗?试说明理由.例2.如图所示,已知在△ABC中,AB=AC=5,BC=6,将△ABC沿BC所在直线向右平移6个单位,得到△DCE,连结AD.(1)请找出图中所有的平行四边形.(2)求四边形ABED的面积.例3如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点,求证:四边形EFGH是菱形.三、随堂练习1.在□ABCD中,(1)若∠A=30°,则∠B=______,∠C=________,∠D=________.(2)若∠A:∠B=1:2,则∠A=______,∠B=_______,∠D=_______.(3)若∠A-∠B=40°,则∠A=______,∠B=_______.(3)若∠A+∠C=90°,则∠D=________.2.如图,在□ABCD中,下列各式不一定正确的是().(A)∠1+∠2=180°;(B)∠2+∠3=180°;(C)∠3+∠4=180°;(D)∠2+∠4=180°3、已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.四、课堂检测1、在□ABCD中,∠ABC的平分线与∠BCD的平分线相交于点O,则∠BOC的度数为2、如图,在菱形ABCD中,AB=BD=5,求:(1)∠BAC的度数;(2)求AC的长。.3已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.⑴求证:AM=DM⑵若DF=2,求菱形ABCD的周长.五、反思与小结AOBCD