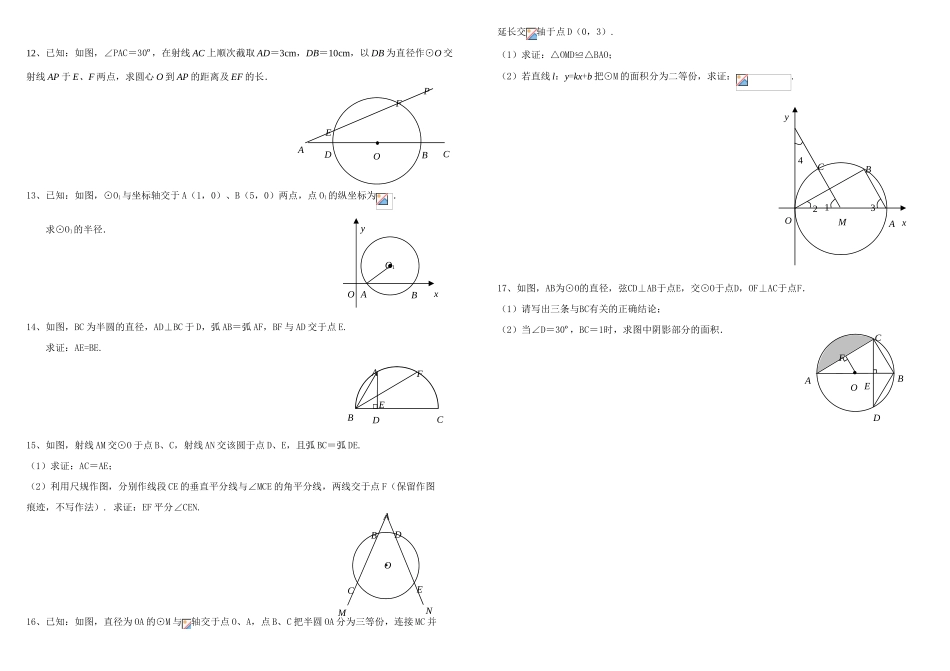
第24章圆的有关性质复习学案班级:_________姓名:__________【考纲解读】(1)理解圆及其有关概念,了解弦、弧、圆心角的关系,掌握垂径定理的应用;(2)探索圆的性质,了解圆周角与圆心角的关系、直径所对的圆周角的特征.【知识要点】1、圆的定义:平面上,到定点的距离等于定长的所有点组成的图形.2、圆的对称性:既是轴对称图形又是中心对称图形.3、圆中的有关概念:(1)弦:连接圆上任意两点间的线段叫做弦,直径是圆中最长的弦.(2)弧:圆上任意两点间的部分叫做弧.(优弧、劣弧、半圆弧)(3)在同圆或等圆中,能够完全重合的弧叫做等弧.(4)圆心角:顶点在圆心的角叫做圆心角.(5)圆周角:顶点在圆上,且两边都与圆相交的角叫做圆周角.4、几个重要性质(1)垂径定理及其逆定理:①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(2)弧、弦、圆心角关系定理:同圆或等圆中,等圆心角对等弧,对等弦.(3)圆周角定理及其推论:①同圆或等圆中,同弧或等弧所对的圆周角相等;②一条弧所对的圆周角等于它所对的圆心角的一半;③半圆(或直径)所对的圆周角是直角,90º的圆周角所对的弦是直径.④圆内接四边形的对角互补,外角等于它的内对角.【实战练习】一、选择题1、如图1,圆心角∠BOC=78º,则圆周角∠BAC的度数是()A.156ºB.78ºC.39ºD.12º2、如图2,△ABC内接于⊙O,若∠OAB=28º,则∠C的大小为()A.28ºB.56ºC.60ºD.62º3、如图3,CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D=50º,则∠C的度数是()A.50ºB.40ºC.30ºD.25º4、如图4,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是()A.1.5B.2C.2.5D.35、如图5,弦CD垂直于⊙O的直径AB,垂足为H,且CD=,BD=,则AB的长为()A.2B.3C.4D.5二、填空题6、如图6,AB为⊙O的直径,CD为⊙O的弦,∠ACD=42º,则∠BAD=______º.7、如图7,A、B、C、D是圆上的点,∠1=70º,∠B=40º,则∠C=______度.8、如图8,一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是________米.9、已知⊙O是△ABC的外接圆,若AB=AC=5,BC=6,则⊙O的半径为________.10、如图9,四边形ABCD内接于⊙O,E是BC延长线上的一点,若∠BOD=100º,则∠DCE=_______º.三、解答题11、如图,在⊙O中,D、E分别为半径OA、OB上的点,且AD=BE.点C为弧AB上一点,连接CD、CE、CO,∠AOC=∠BOC.求证:CD=CE.图2图1ABCO图3CADOECABO图4图5ABODECABCD1图7图8图6ADOBCE图912、已知:如图,∠PAC=30º,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.13、已知:如图,⊙O1与坐标轴交于A(1,0)、B(5,0)两点,点O1的纵坐标为.求⊙O1的半径.14、如图,BC为半圆的直径,AD⊥BC于D,弧AB=弧AF,BF与AD交于点E.求证:AE=BE.15、如图,射线AM交⊙O于点B、C,射线AN交该圆于点D、E,且弧BC=弧DE.(1)求证:AC=AE;(2)利用尺规作图,分别作线段CE的垂直平分线与∠MCE的角平分线,两线交于点F(保留作图痕迹,不写作法).求证:EF平分∠CEN.16、已知:如图,直径为OA的⊙M与轴交于点O、A,点B、C把半圆OA分为三等份,连接MC并延长交轴于点D(0,3).(1)求证:△OMD≌△BAO;(2)若直线l:y=kx+b把⊙M的面积分为二等份,求证:.17、如图,AB为⊙O的直径,弦CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.(1)请写出三条与BC有关的正确结论;(2)当∠D=30º,BC=1时,求图中阴影部分的面积.ABCODEMNCBAOFDEABCDEFOADBCEFPxAO1OByyxCBAMO4213