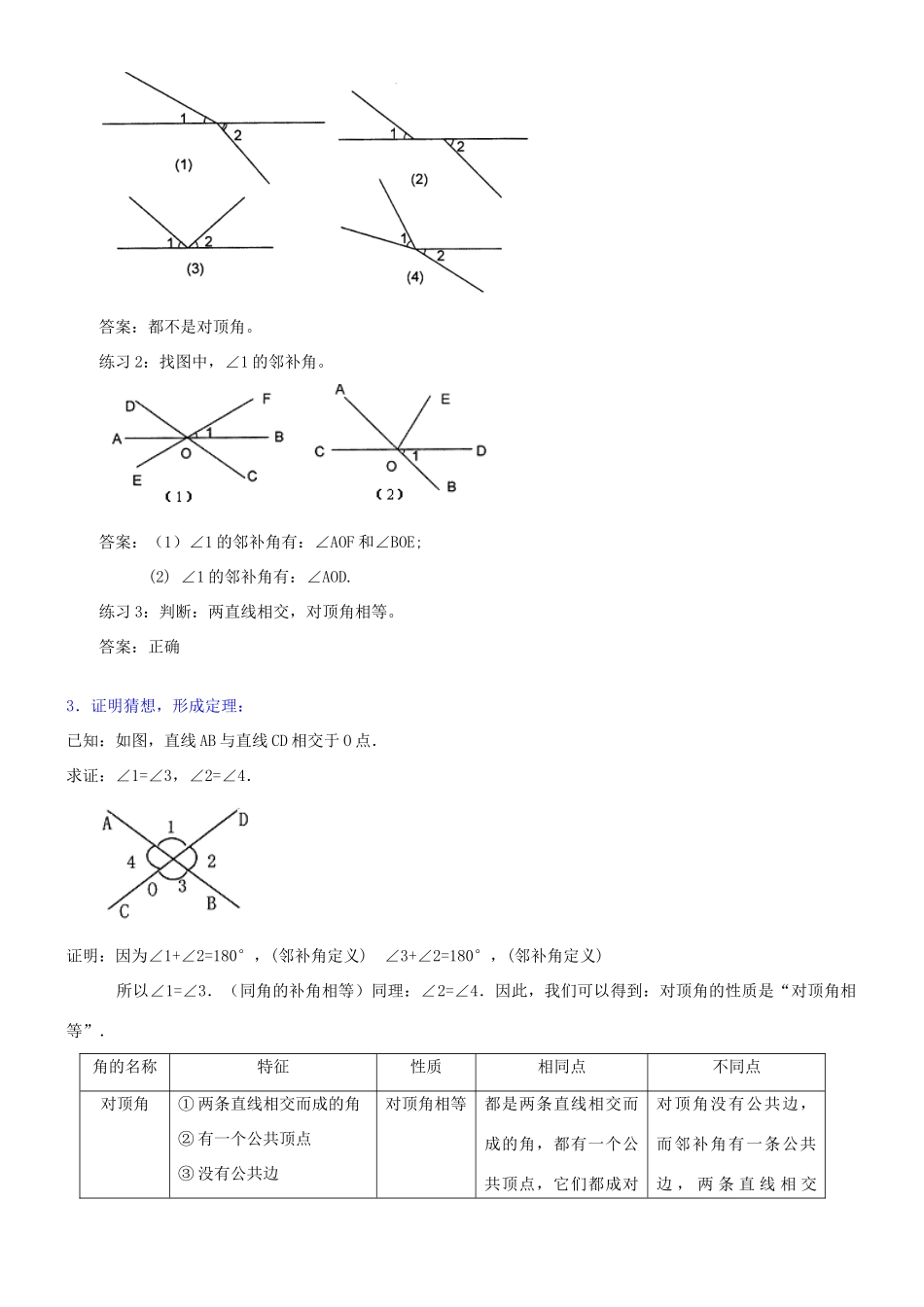
相交线与平行线复习教案一.学习目标及重难点处理(一)学习目标:“平面内两条直线的位置关系”是“空间与图形”知识方法体系发展中的基本问题.知识结构如下图所示:(二)重难点处理:是垂线的概念与平行线的判定和性质以及平移内容,因为这些知识是空间与图形领域的基础知识,在以后的学习中经常要用到,这部分内容掌握不好,将会影响后续内容的学习.直线的位置关系是通过有关角的知识反映出来的,理解好与相交线、平行线有关的角的知识:对项角、邻补角、三线八角。二.学习目标及重难点处理(一)、对顶角和邻补角的概念1.概念:在相交的两条直线得到的四个角中,(1)有公共顶点,没有公共边的两个角叫做对顶角。如图中的∠1和∠2,∠3和∠4。(2)有一个公共顶点,还有一条公共边的两个角叫做邻补角。如图中的∠1与∠3,∠2和∠4。邻补角也可以看成是:一条直线与端点在这条直线的一条射线组成的两个角。指出:邻补角是两个角互补的特殊关系,如下图。2.练习:练习1:辨别图形:下图中两角是对顶角吗?答案:都不是对顶角。练习2:找图中,∠1的邻补角。答案:(1)∠1的邻补角有:∠AOF和∠BOE;(2)∠1的邻补角有:∠AOD.练习3:判断:两直线相交,对顶角相等。答案:正确3.证明猜想,形成定理:已知:如图,直线AB与直线CD相交于O点.求证:∠1=∠3,∠2=∠4.证明:因为∠1+∠2=180°,(邻补角定义)∠3+∠2=180°,(邻补角定义)所以∠1=∠3.(同角的补角相等)同理:∠2=∠4.因此,我们可以得到:对顶角的性质是“对顶角相等”.角的名称特征性质相同点不同点对顶角①两条直线相交而成的角②有一个公共顶点③没有公共边对顶角相等都是两条直线相交而成的角,都有一个公共顶点,它们都成对对顶角没有公共边,而邻补角有一条公共边,两条直线相交出现。时,一个角的对顶角有一个,一个角的邻补角有两个。邻补角①两条直线相交而成的角②有一个公共顶点③有一条公共边邻补角互补4.例题:例.如图,(1)已知直线AB,CD相交于点0,(2)已知直线AE,BD相交于点C.图中哪些角是邻补角?哪些角是对顶角?答:(1)邻补角是∠DOA与∠AOC,∠AOE与∠EOB,∠BOC与∠COA,∠COE与∠DOE,∠DOA与∠DOB,∠DOB与∠BOC;对顶角是∠AOD与∠COB.∠AOC与∠DOB。(2)邻补角是∠ACB与∠ACD,∠ECD与∠DCA,∠DCE与∠ECB,∠ECB与∠ACB;对顶角是∠ACB与∠DCE,∠BCE与∠ACD.(二)、垂直1.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。它们的交点叫做垂足。2.垂线的性质:过一点有且只有一条直线与已知直线垂直。(1)“过一点”有几种情况?(2)“有且只有”什么意思?答案:(1)此点在直线上或直线外;(2)存在性和唯一性。3.练习:过点P分别向角的两边作垂线。答案:略(三)、同位角、内错角、同旁角的概念1.概念:角的名称位置特征基本图形图形结构特征同位角在两条被截直线同旁,在截线同侧去掉多余的线体现基本图形形如字母“F”(或倒“F”形)内错角在两条被截直线之内,在截线两侧(交错)去掉多余的线体现基本图形形如字母“Z”(或反置)同旁内角在两条被截直线之内,在截线同侧去掉多余的线体现基本图形形如字母“U”2.练习:练习1、如图1,找出右图中所有的同位角、内错角、同旁内角。答案:(1)同位角:∠1与∠6,∠2与∠5,∠3与∠6,∠4与∠7;内错角:∠1与∠6,∠4与∠5;同旁内角:∠1与∠5,∠4与∠6.(2)同位角:∠1与∠3,∠2与∠4;内错角:无;同旁内角:∠2与∠3.练习2、如图2,直线a、b被直线c所截的角中,找出同位角、内错角、同旁内角。答案:(1)同位角:∠1与∠5,∠2与∠6,∠3与∠8,∠4与∠7;内错角:∠2与∠8,∠4与∠5;同旁内角:∠2与∠5,∠4与∠8.(四)直线平行的条件1.三线八角:先结合生产实践中工匠师傅们的经验做法,探求其理论实质,在下列图示中辨认‘三线八角’:2.直线的平行(重点知识讲解):(1)平行线的概念:在同一平面内,不相交的两条直线叫做平行线.若两条直线a,b互相平行,记作a∥b.强调两条直线不重合。(2)平行公理:经过直线外一点有且只有一条直线和这...