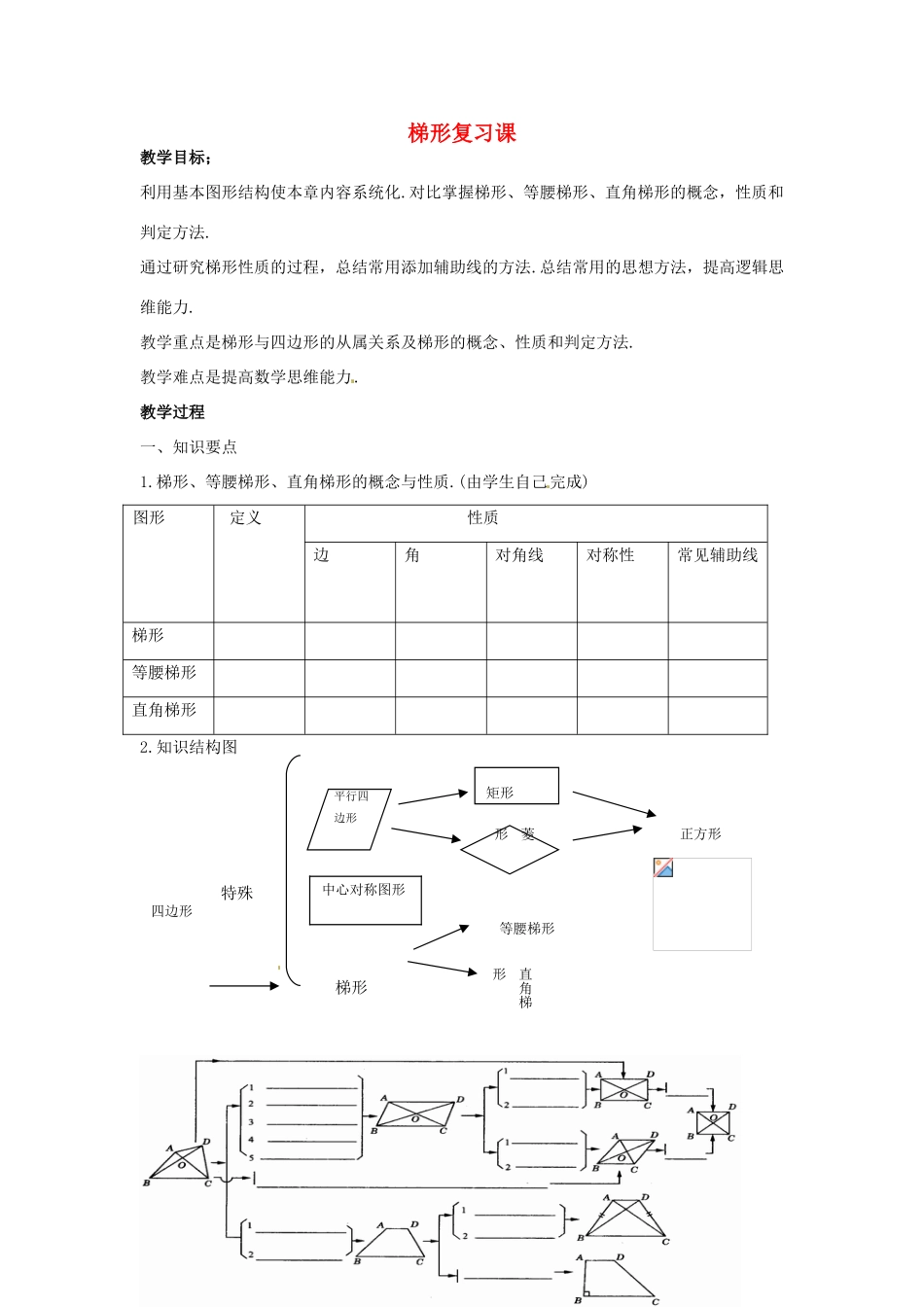
梯形复习课教学目标;利用基本图形结构使本章内容系统化.对比掌握梯形、等腰梯形、直角梯形的概念,性质和判定方法.通过研究梯形性质的过程,总结常用添加辅助线的方法.总结常用的思想方法,提高逻辑思维能力.教学重点是梯形与四边形的从属关系及梯形的概念、性质和判定方法.教学难点是提高数学思维能力.教学过程一、知识要点1.梯形、等腰梯形、直角梯形的概念与性质.(由学生自己完成)图形[来源:学,科,网Z,X,X,K][来源:Zxxk.Com]定义[来源:Zxxk.Com][来源:Zxxk.Com][来源:Zxxk.Com][来源:学科网][来源:学#科#网]性质[来源:学§科§网Z§X§X§K][来源:学科网][来源:学科网][来源:学&科&网]边角对角线对称性常见辅助线梯形等腰梯形直角梯形2.知识结构图4.在下列图表中,用符号语言写出判定某种特殊四边形的各种条件:四边形梯形等腰梯形直角梯形矩形特殊平行四边形菱形正方形中心对称图形说明:课前,教师可把上面的表图印发给学生,以便当堂看图填空。填写此表,有助于学生从“整体”上把握各种特殊四边形的判定方法,并能较好地掌握其中的联系与区别。二、典型例题分析例1填出右图中各图形的名称,分清各四边形之间的关系,巩固判定一个梯形是等腰梯形的方法.2.等腰梯形的性质的应用,总结证明两条线段相等的方法和添加辅助线的方法及分析综合法的使用.例2已知:如图,在梯形ABCD中,AB∥CD,以AD和AC为边作ACED,DC的延长交EB于F.求证:EF=FB.分析:(1)分解基本图形:“ACED及对角线”,三个梯形.(2)应用分析综合法探求解题思路,添加辅助线,将EF,FB放在“证明两线段相等”所对应的基本图形中.(3)总结目前证明两条线段相等的方法,添设相应的辅助线.特殊四边形的边、对角线的性质;平行线间的距离相等;过三角形一边的中点与底边平行的直线必平分第三边;过梯形一腰的中点与底边平行的直线必平分另一腰.(补充)说明:本题添加辅助线分为四大类.(1)构造三角形中位线或梯形中位线.(延长EC交AB于G)(作EG∥DC交AD延长线于G)(联结AE)(作DG∥AC交BA延长线于G)(2)构造全等的三角形(3)构造等腰三角形作FG=FB,联结EG.(4)构造以EB为对角线的平行四边形3.总结梯形中常用的辅助线,掌握化归的思想.梯形中添加辅助线常常可以将梯形化归为三角形、平行四边形、矩形、直角梯形等.同时,还可以集中梯形中分散的已知条件,如右图中将梯形的两腰、两底角、两边之差集中到了一个三角形中.另外还要注意:(1)从图形变换及化归角度理解梯形中常用辅助线的作法及作用.平移旋转对称(2)其它几种作法.一般梯形中,过上底两端点作下底的垂线;向上延长两腰构成三角形;作FG∥CA作EG┴DF,BH┴DF作FG∥DA例3已知:如图,在梯形ABCD中,AB∥CD,AC┴DB,AD=BC=4,ADC=60°,E,F分别是AD,BC的中点,EF交BD于M,交AC于N.(1)求EF、MN的长及S梯形ABCD;(2)观察MN的长与梯形上、下底的关系,并思考结论能否推广到一般梯形?分析:本题可采用(1)(2)中辅助线的作法,解得EF=2,MN=2,S梯形ABCD=12,MN=三、师生共同小结1.基本方法.(1)利用基本图形结构使知识系统化;(2)证明两条线段相等的方法及和差关系的方法,两线垂直、平行的方法.(3)利用变换的思想添加辅助线的方法.(4)探究解题思路时的分析、综合法.2.基本思想及观点:(1)“特殊---一般---特殊”认识事物的方法;(2)化归的思想;四、作业板书设计:(1)(2)1.梯形、等腰梯形、直角梯形的概念与性质.图形定义性质边角对角线对称性常见辅助线梯形等腰梯形直角梯形例2已知:如图,在梯形ABCD中,AB∥CD,以AD和AC为边作ACED,DC的延长交EB于F.求证:EF=FB.