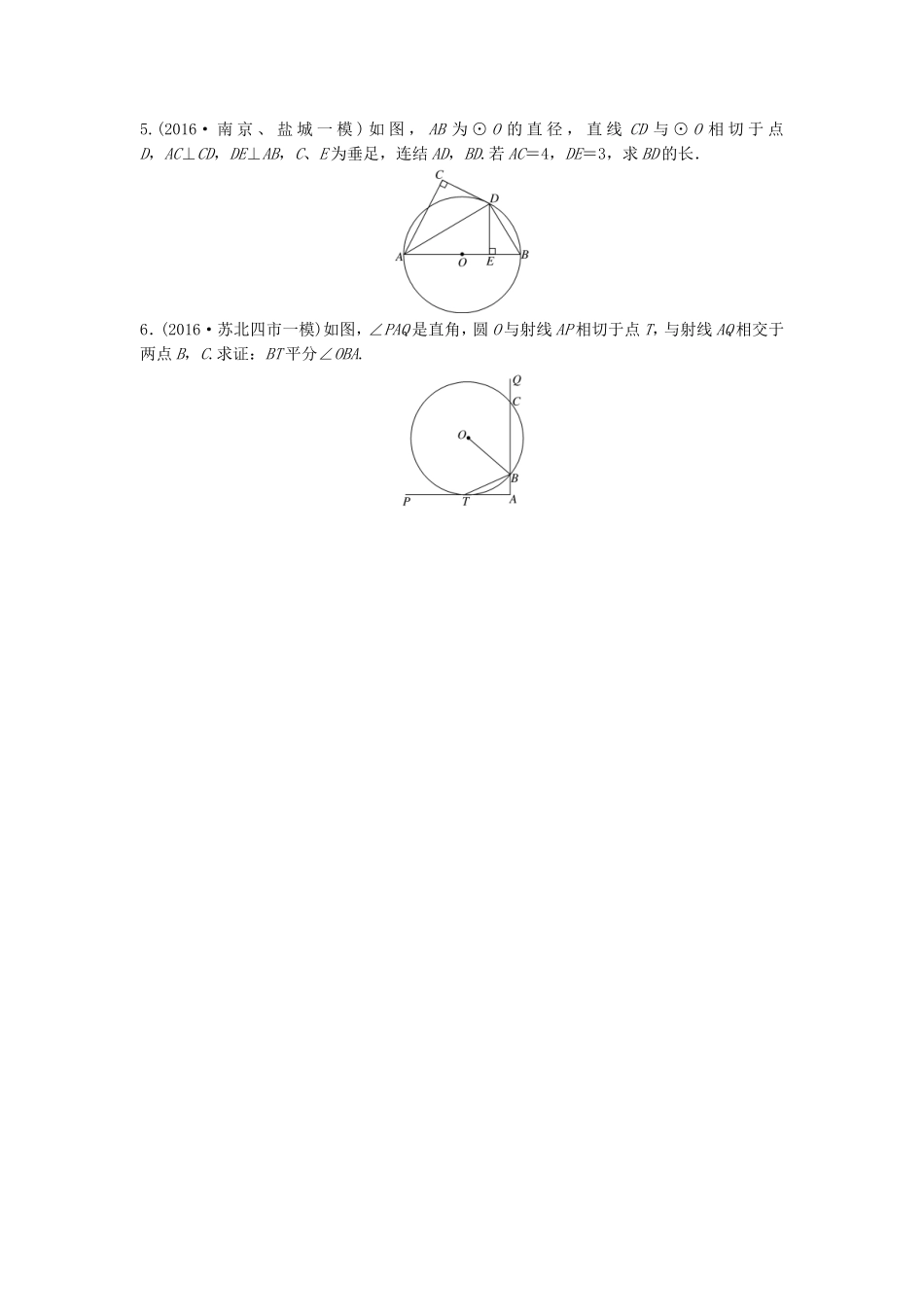
训练目标在初中平面几何的基础上进一步掌握有关平面几何证明的定理或方法.训练题型(1)证明三角形相似及相似三角形的性质;(2)圆的切线的判定与性质;(3)相交弦定理、切割线定理的应用.解题策略回忆初中学过的平面几何有关的定义、定理、推论等,理解高中新给出的结论,充分利用图形,解决相关问题.1.如图所示,在△ABC中,D是AC的中点,E是BD的中点,AE的延长线交BC于F.(1)求的值;(2)若△BEF的面积为S1,四边形CDEF的面积为S2,求S1∶S2的值.2.(2016·南京六校联考)如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.求证:FG∥AC.3.(2016·南京、盐城一模)如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D.若PA=18,PC=6,求线段CD的长.4.(2016·南通三模)如图,BC为圆O的直径,A为圆O上一点,过点A作圆O的切线交BC的延长线于点P,AH⊥PB于H.求证:PA·AH=PC·HB.5.(2016·南京、盐城一模)如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连结AD,BD.若AC=4,DE=3,求BD的长.6.(2016·苏北四市一模)如图,∠PAQ是直角,圆O与射线AP相切于点T,与射线AQ相交于两点B,C.求证:BT平分∠OBA.答案精析1.解(1)过D点作DG∥BC,交AF于G点.∵E是BD的中点,∴BE=DE.又∵∠EBF=∠EDG,∠BEF=∠DEG,∴△BEF≌△DEG,∴BF=DG,∴BF∶FC=DG∶FC.∵D是AC的中点,∴DG∶FC=1∶2,∴BF∶FC=1∶2,即=.(2)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF∶BC=1∶3,又由BE∶BD=1∶2,可知h1∶h2=1∶2,其中h1,h2分别为△BEF和△BDC的高,则=×=,则S1∶S2=1∶5.2.证明∵AB为切线,AE为割线,∴AB2=AD·AE,又∵AC=AB,∴AD·AE=AC2.∴=,又∵∠EAC=∠CAD,∴△ADC∽△ACE,∴∠ADC=∠ACE,又∵∠ADC=∠EGF,∴∠EGF=∠ACE,∴GF∥AC.3.解由切割线定理,得PC2=PA·PB,解得PB=2,所以AB=16,所以Rt△ABC的外接圆半径r=8,记Rt△ABC外接圆的圆心为O,连结OC,则OC⊥PC,在Rt△POC中,由面积法得OC·PC=PO·CD,解得CD=.4.证明连结AC,AB,因为BC为圆O的直径,故AC⊥AB.又AH⊥PB,故AH2=CH·HB,即=.因为PA为圆O的切线,故∠PAC=∠B.在Rt△ABC中,∠B+∠ACB=90°,在Rt△ACH中,∠CAH+∠ACB=90°,所以∠CAH=∠B,所以∠PAC=∠CAH,所以=,即=.所以=,即PA·AH=PC·HB.5.解因为CD与⊙O相切于点D,所以∠CDA=∠DBA,因为AB为⊙O的直径,所以∠ADB=90°.又DE⊥AB,所以△EDA∽△DBA,所以∠EDA=∠DBA,所以∠EDA=∠CDA,=.又∠ACD=∠AED=90°,AD=AD,所以△ACD≌△AED.所以AE=AC=4,所以AD==5,又=,所以BD=·AD=.6.证明连结OT.因为AT是切线,所以OT⊥AP.又因为∠PAQ是直角,即AQ⊥AP,所以AB∥OT,所以∠TBA=∠BTO.又OT=OB,所以∠OTB=∠OBT,所以∠OBT=∠TBA,即BT平分∠OBA.