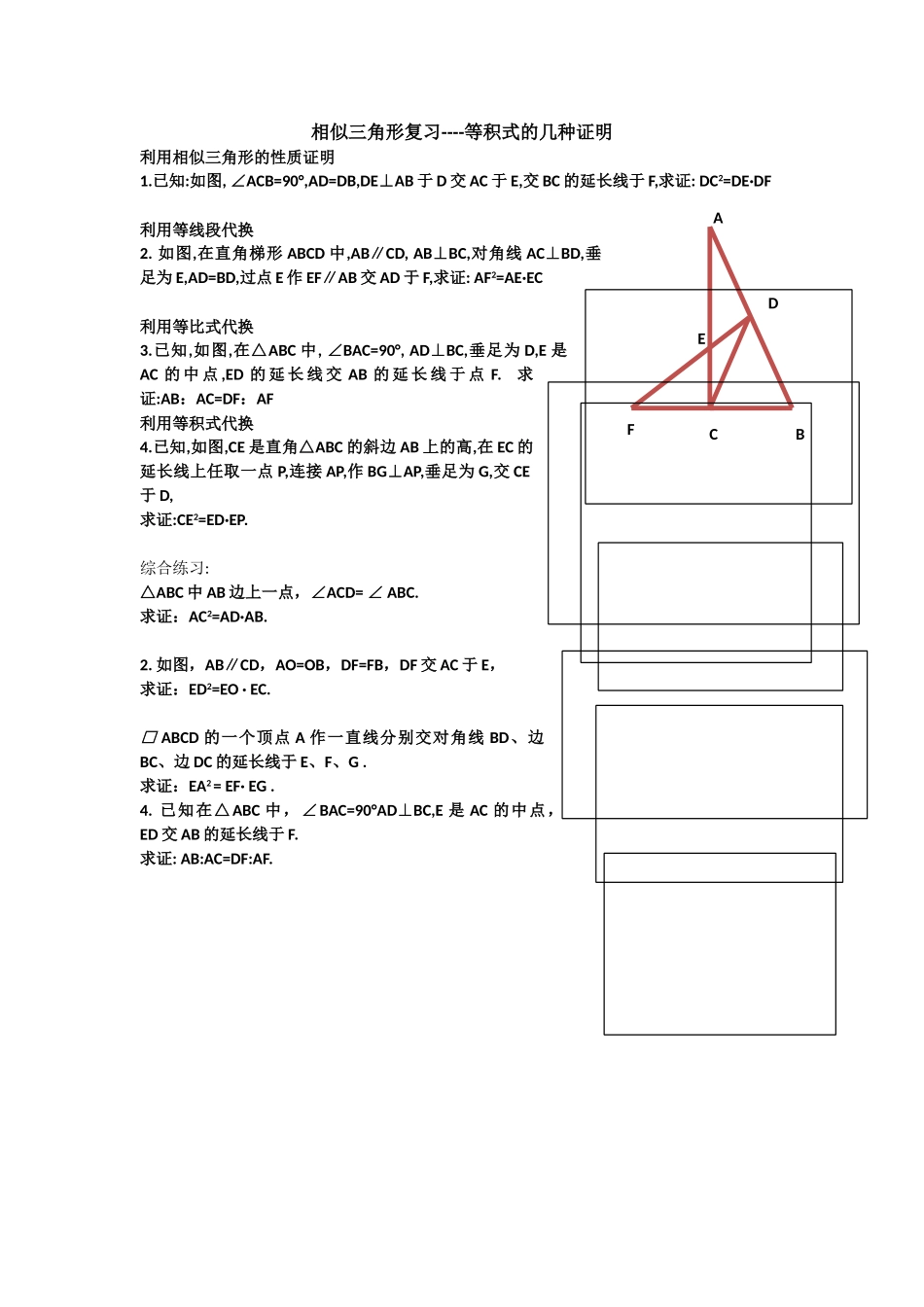
相似三角形复习----等积式的几种证明利用相似三角形的性质证明1.已知:如图,∠ACB=90°,AD=DB,DE⊥AB于D交AC于E,交BC的延长线于F,求证:DC2=DE·DF利用等线段代换2.如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD,过点E作EF∥AB交AD于F,求证:AF2=AE·EC利用等比式代换3.已知,如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:AB:AC=DF:AF利用等积式代换4.已知,如图,CE是直角△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D,求证:CE2=ED·EP.综合练习:△ABC中AB边上一点,∠ACD=∠ABC.求证:AC2=AD·AB.2.如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,求证:ED2=EO·EC.□ABCD的一个顶点A作一直线分别交对角线BD、边BC、边DC的延长线于E、F、G.求证:EA2=EF·EG.4.已知在△ABC中,∠BAC=90°AD⊥BC,E是AC的中点,ED交AB的延长线于F.求证:AB:AC=DF:AF.ADBFCE