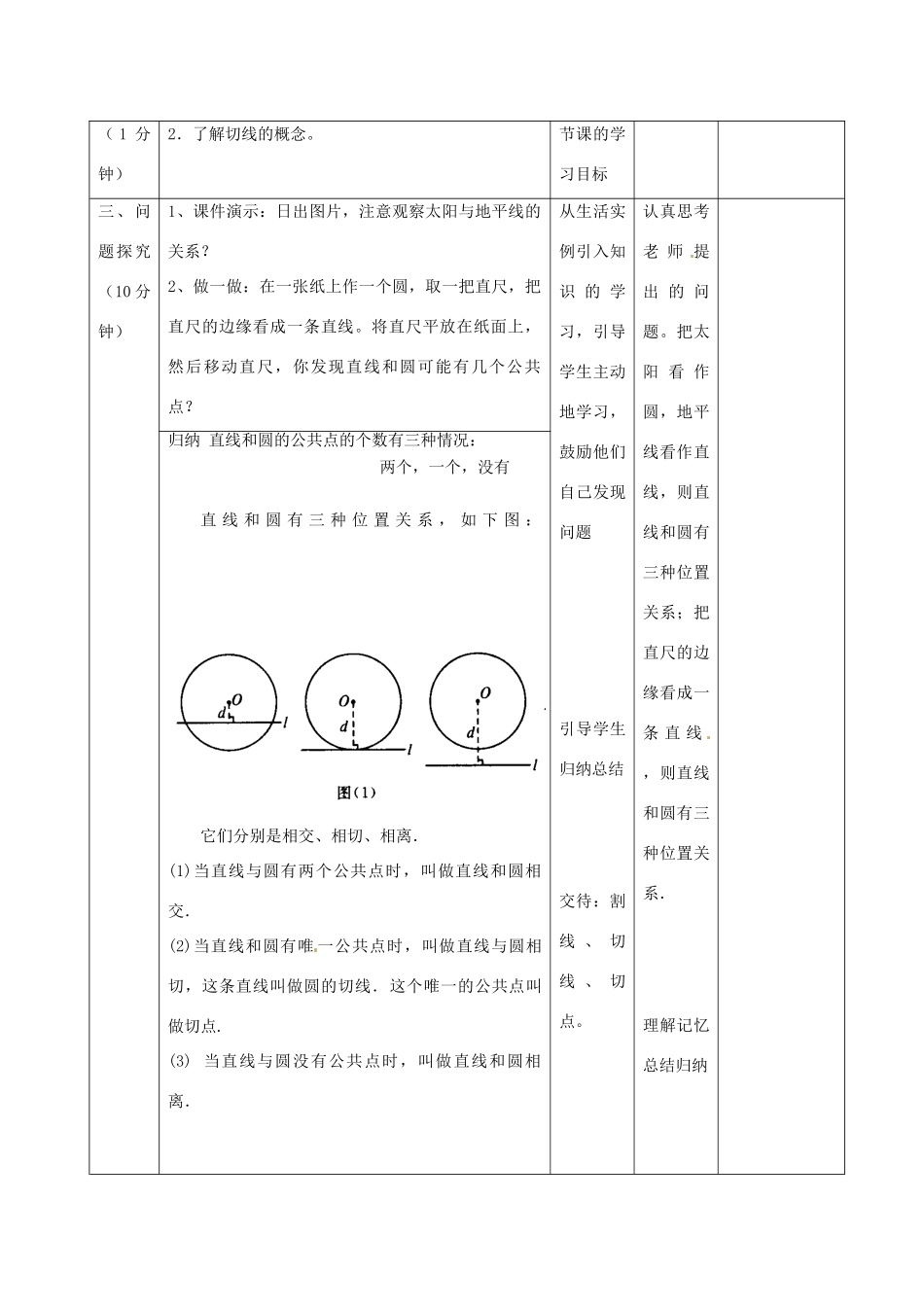
《直线和圆的位置关系》教学设计【课标分析】理解直线与圆有相交、相切、相离三种位置关系:了解切线的概念。【教材分析】这部分内容包括直线和圆的三种关系,探索圆的切线的性质,探索圆的切线的判定方法,以及作三角形内切圆的方法。探索并证明切线长定理,并运用切线长定理进行有关的论证和计算。本节课主要研究直线和圆的三种位置关系。【学生分析】首先让学生感受生活中反映直线与圆位置关系的现象,然后让学生动手操作,在这一过程中引导学生归纳出直线与圆的几种位置关系,进一步归纳出直线与圆的不同位置关系中d与r的大小关系,然后对d=r的情形特别关注,这就是圆和直线的相切关系,从而讨论得出切线的性质,再通过旋转实验的办法探索切线的判定条件。在此基础上能做出三角形的内切圆。在教学中主要让学生探索归纳,当遇到困难时教师给予适当指导,这样可以充分发挥学生的主观能动性,还能增进同学们的友谊,培养学生的合作能力。【教学过程】教学流程教师活动设计设计目的学生活动设计二次备课一、导入新课(2分钟)我们在前面学过点和圆的位置关系,请大家回忆它们的位置关系有哪些?(1)点在圆外d>r;(2)点在圆上d=r;(3)点在圆内d<r。直线与圆的位置关系有哪些情况呢?本节课我们类比着来学习。(板书课题:《直线和圆的位置关系》)复习引入为本节课的学习打好基础学生思考并回答问题二、目标定向1.经历探索直线与圆位置关系的过程,理解直线与圆有相交、相切、相离三种位置关系.旨在让学生明确本明确目标做好准备(1分钟)2.了解切线的概念。节课的学习目标三、问题探究(10分钟)1、课件演示:日出图片,注意观察太阳与地平线的关系?2、做一做:在一张纸上作一个圆,取一把直尺,把直尺的边缘看成一条直线。将直尺平放在纸面上,然后移动直尺,你发现直线和圆可能有几个公共点?从生活实例引入知识的学习,引导学生主动地学习,鼓励他们自己发现问题引导学生归纳总结交待:割线、切线、切点。认真思考老师提出的问题。把太阳看作圆,地平线看作直线,则直线和圆有三种位置关系;把直尺的边缘看成一条直线,则直线和圆有三种位置关系.理解记忆总结归纳归纳直线和圆的公共点的个数有三种情况:两个,一个,没有直线和圆有三种位置关系,如下图:它们分别是相交、相切、相离.(1)当直线与圆有两个公共点时,叫做直线和圆相交.(2)当直线和圆有唯一公共点时,叫做直线与圆相切,这条直线叫做圆的切线.这个唯一的公共点叫做切点.(3)当直线与圆没有公共点时,叫做直线和圆相离.让学生举出生活中的实例,有助于学生对于三种位置关系的理解。位置关系转化为数量关系。从自己的生活体验中举出满足条件的实例。类比点和圆的位置关系进行总结。议一议:你能举出生活中直线与圆相交、相切、相离的实例吗?举例:如(1)把一只筷子放在碗上,把碗看作圆,筷子看作直线,这时直线与圆相交;(2)自行车的轮胎在地面上滚动,车轮为圆,地平线为直线,这时直线与圆相切;(3)杂技团中骑自行车走钢丝中的自行车车轮为圆,地平线为直线,这时直线与圆相离.等等。想一想:能否根据点和圆的位置关系,点到圆心的距离d和半径r作比较,类似地推导出如何用点到直线的距离d和半径r之间的关系来确定三种位置关系呢?圆心O到直线l的距离为d,圆的半径为r,当直线与圆相交时dr,因此可以用d与r间的大小关系断定直线与圆的位置关系.四、总结归纳(2分钟)判断直线与圆的位置关系有两种方法.一种是从直线与圆的公共点的个数来断定;一种是用d与r的大小关系来断定.(1)从公共点的个数来判断;直线与圆有两个公共点时,直线与圆相交;直线与圆有唯一公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.(2)从点到直线的距离(d与半径r的大小关系)来判进行归纳总结,明确判断依据。及时进行归纳总结,明确等价关系。断:d1、圆的直径是13cm,如果直线与圆心的距离分别(1)4.5cm(2)6.5cm(3)8cm那么直线和圆分别是什么位置关系?有几个公...