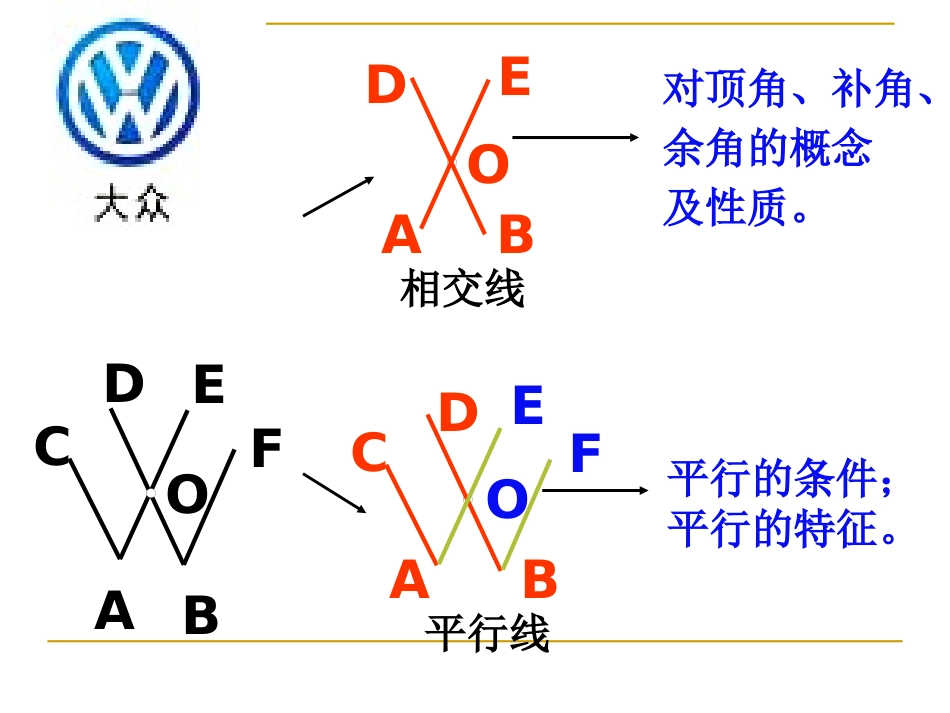
第二章平行线与相交线回顾与思考ABCDEFOABDEO相交线ABCD对顶角、补角、余角的概念及性质。平行的条件;平行的特征。FEO平行线概念、性质填空:一、概念:两个角的和是_____,称这两个角互为余角。两个角的和是平角,称这两个角互为_____。有公共顶点,两边互为反向延长线的两个角叫做_______。二、性质:•_________的余角相等;•同角或等角的____相等;•对顶角_____。直角补角对顶角同角或等角补角相等三线八角:两条直线AB与CD被第三条直线EF所截,形成:(1)同位角:(2)内错角:(3)同旁内角:同位角是同位角是FF形状形状内错角是内错角是ZZ形状形状同旁内角是同旁内角是UU形状形状CCAA11337755228866EE44DDBBF区别:条件与结论互换,即:已知平行用特征,探索平行用判定。一、平行线的判定方法:•同位角相等,两直线平行;•内错角相等,两直线平行;•同旁内角互补,两直线平行;二、平行线的特征:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。87654321ab知识结构图:相交线与平行线相交线平行线补角、余角、对顶角丰富情景探索直线平行的特征探索直线平行的条件同位角内错角同旁内角二、强化知识、技能训练1.(1)若∠1=50°,则∠2=_______∠BOC=_______。OABCD21(2)若∠BOC=21∠,则∠1=______∠BOC=_______。(3)若OEAB⊥,∠1=56°,则∠3=_____。60°120°34°50°130°3E2.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程)ADBC115°110°解:∵AD∥BC,∠A=115°,∠D=110°(已知)∴∠A+∠B=180°∠D+∠C=180°(两直线平行,同旁内角互补)∴∠B=180°﹣115°=65°∠C=180°-110°=70°3.图中如果AC∥BD、AE∥BF,那么∠A与∠B的关系如何?你是怎样思考的?ABCDEFO解:∵AC//BD,AE//BF(已知)∴∠A=DOE∠∠B=DOE∠(两直线平行,同位角相等)∴∠A=B(∠等量代换)4.已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°求证:AB//CDABCDEF12HG证明:解一:∵∠1+EHB=180°∠(平角的定义)∠1+2=180°(∠已知)∴∠EHB=2∠(同角的补角相等)∴AB//CD(同位角相等,两直线平行)解二:∵∠1+AHG=180°∠(平角的定义)∠1+2=180°(∠已知)∴∠AHG=2∠(同角的补角相等)∴AB//CD(内错角相等,两直线平行)解三:∵∠1=BHG(∠对顶角相等)∠1+2=180°∠(已知)∴∠BHG+2=180°∠(等量代换)∴AB//CD(同旁内角互补,两直线平行)证明:∵BD平分∠ABC(已知)∴∠2=3(∠角平分线定义)又∵∠2=1∠(已知)∴∠3=1∠(等量代换)∴ADBC∥(内错角相等,两直线平行)5.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC.ABCD1236.如图已知∠1=∠ACB,∠2=∠3.求证:CD∥FH.(小明写了相关的过程,但是却忘了写理由请你帮他把理由补充完整)解:∵∠1=∠ACB(已知)∴DEBC∥()∴∠2=DCF∠()又∵∠2=∠3(已知)∴∠3=DCF∠()∴CDFH∥()HACBFDE123同位角相等,两直线平行两直线平行,内错角相等等量代换同位角相等,两直线平行7.如图已知AD∥BC,且DC⊥AD于D.(1)DC与BC有怎样的位置关系?说说你的理由。(2)你能说明∠1+2=180°∠吗?ADCB1243解:(1)∵DCAD⊥于D(已知)∴∠3=90°(垂直定义)又∵ADBC∥(已知)∴∠3+DCB=180°∠(两直线平行,同旁内角互补)∴∠DCB=180°-90°=90°因此,DCBC⊥ADCB1243(2)解:∵AD//BC(已知)∴∠2+4=180°∠(两直线平行,同旁内角互补)又∵∠1=4∠(对顶角相等)∴∠1+2=180∠°(等量代换)8.如图,已知AB//CD(1)你能找到∠B、∠D和∠BED的关系吗?(2)如果∠B=46,∠D=58,则∠E的度数是多少?ABCDE