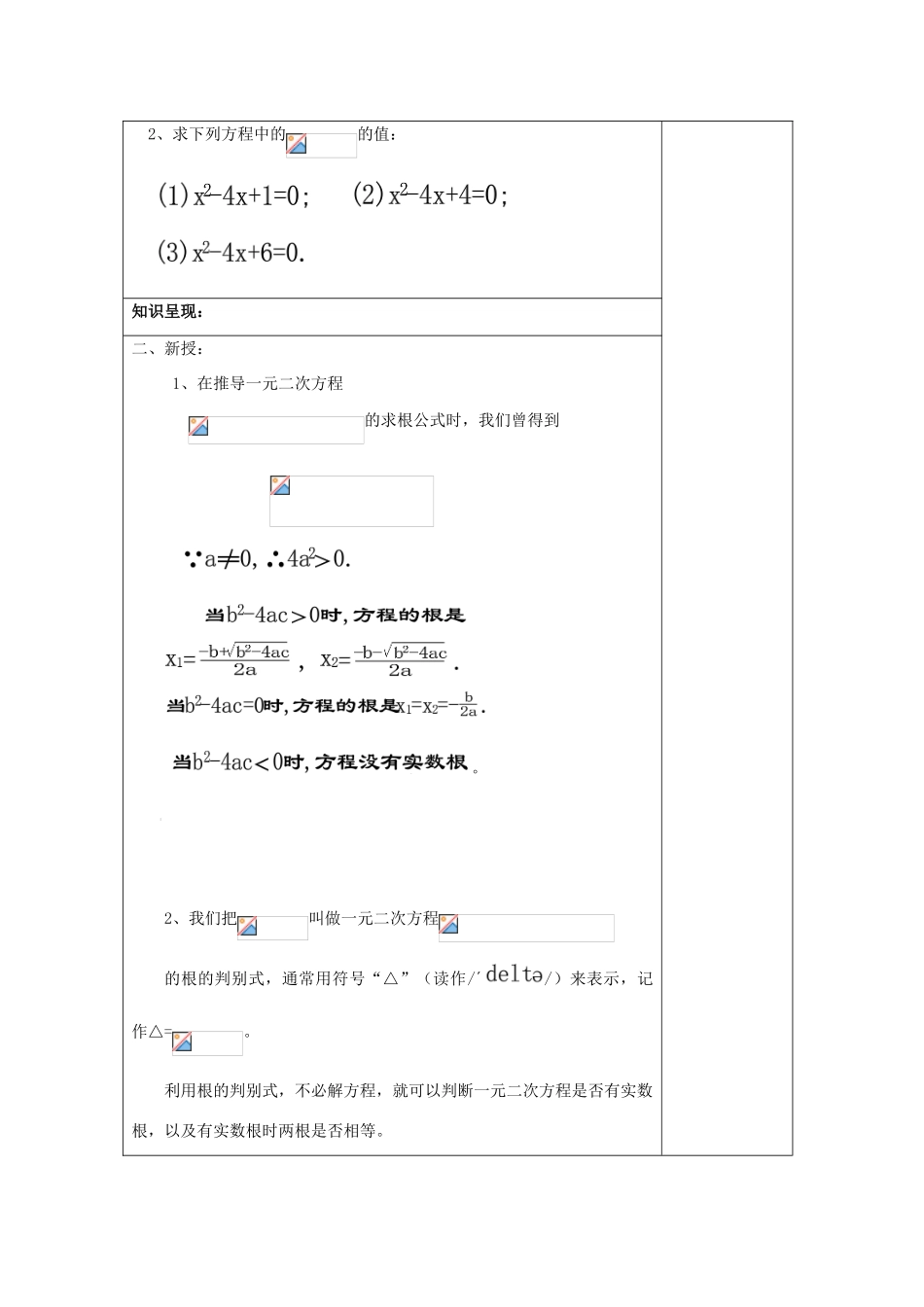
一元二次方程根的判别式课题17.3(1)一元二次方程根的判别式设计依据(注:只在开始新章节教学课必填)教材章节分析:学生学情分析:课型新授课教学目标1、会根据根的判别式判断一元二次方程根的情况,会根据元二次方程根的情况确定方程中一个字母系数的取值范围.2、经历一元二次方程根的判别式概括过程,通过从具体到抽象的认识活动,渗透分类讨论的思想;培养学生观察,比较,分析,综合,抽象概括能力.3、通过一元二次方程的系数与方程根的分布两者的互相制约,对学生进行辩证唯物主义观点教育,激发学生的学习积极性和主动性.重点经历一元二次方程根的判别式的导出过程,会根据根的判别式判断一元二次方程根的情况.难点一元二次方程根的判别式的应用中的“说明”题.教学准备多媒体教学学生活动形式讨论,交流,总结,练习教学过程设计意图课题引入:一、复习:1、用开平方法解下列方程:2、求下列方程中的的值:知识呈现:二、新授:1、在推导一元二次方程的求根公式时,我们曾得到。2、我们把叫做一元二次方程的根的判别式,通常用符号“△”(读作/´/)来表示,记作△=。利用根的判别式,不必解方程,就可以判断一元二次方程是否有实数根,以及有实数根时两根是否相等。3、一元二次方程,当△=>0时,方程有两个不相等的实数根;当△==0时,方程有两个相等的实数根;当△=<0时,方程没有实数根。当方程没有实数根时,△<0。上述判断反过来说,也是正确的,即:当方程有两个不相等的实数根时,△>0;当方程有两个相等的实数根时,△=0;4、例题1不解方程,判别下列方程的根的情况:例题2关于x的方程(其中m是实数)一定有实数根吗?为什么?三、巩固练习:1、不解方程,判断下列方程的根的情况:2、关于x的方程(其中)一定有实数根吗?为什么?3、思考一元二次方程,当的符号在什么情况下,不通过计算的值,就可以判断方程一定有两个不相等的实数根。课堂小结:四、本课小结:一元二次方程根的判别式1、根的判别式:叫做一元二次方程的根的判别式,用符号“△”来表示。记作△=2、一元二次方程,当△=>0时,方程有两个不相等的实数根;当△==0时,方程有两个相等的实数根;当△=<0时,方程没有实数根。上述判断反过来说,也是正确的,即:当方程有两个不相等的实数根时,△>0;当方程有两个相等的实数根时,△=0;当方程没有实数根时,△<0。课外作业练习册P:24习题17.3(1)预习要求17.3(2)一元二次方程根的判别式教学后记与反思1、课堂时间消耗:教师活动15分钟;学生活动25分钟)2、本课时实际教学效果自评(满分10分):分3、本课成功与不足及其改进措施: